Mathematics
A 7 m long flagstaff is fixed on the top of a tower. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 45° and 36° respectively. Find the height of the tower correct to one place of decimal.
Heights & Distances
52 Likes
Answer
Let CD be the tower of height h meters and BD the flagstaff.
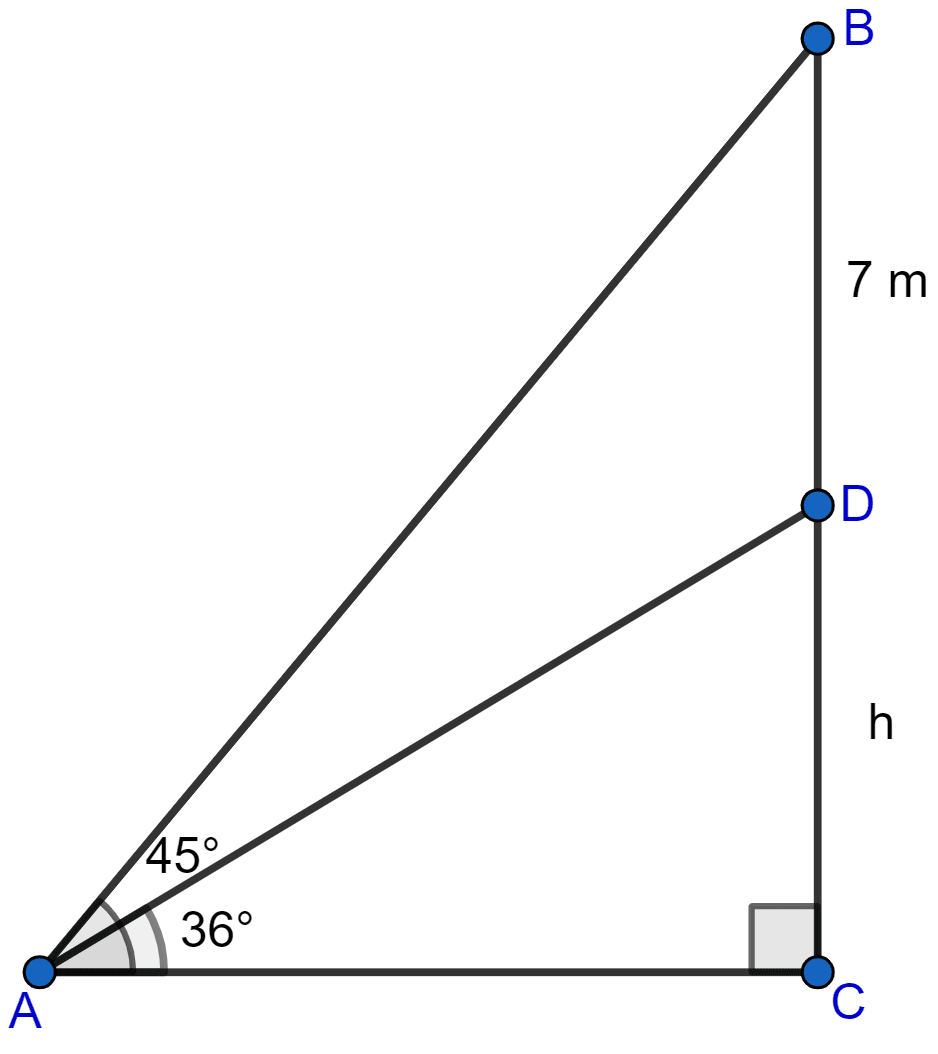
A be point on the ground from where the angles of elevation of the top and bottom of the flagstaff are 45° and 36° respectively.
From figure,
BC = BD + DC = (7 + h) meters.
Considering right angled triangle △ABC,
Considering right angled triangle △ADC,
Putting value of AC in Eq 1 we get,
Hence, the height of tower is 18.6 m.
Answered By
20 Likes
Related Questions
The angle of elevation of the top of a tower from a point A (on the ground) is 30°. On walking 50 m towards the tower, the angle of elevation is found to be 60°. Calculate :
(i) the height of the tower (correct to one decimal place)
(ii) the distance of the tower from A.
An aeroplane 3000 m high, passes vertically above another aeroplane at an instant when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the two planes.
A boy, 1.6 m tall, is 20 m away from a tower and observes that the angle of elevation of the top of the tower is 60. Find the height of the tower.
A boy 1.54 m tall can just see the sun over a wall 3.64 m high which is 2.1 m away from him. Find the angle of elevation of the sun.