KnowledgeBoat Logo
|

Mathematics

A boy, 1.6 m tall, is 20 m away from a tower and observes that the angle of elevation of the top of the tower is 60. Find the height of the tower.

Heights & Distances

27 Likes

Answer

Let AD be man and BC be tower of height h meters.

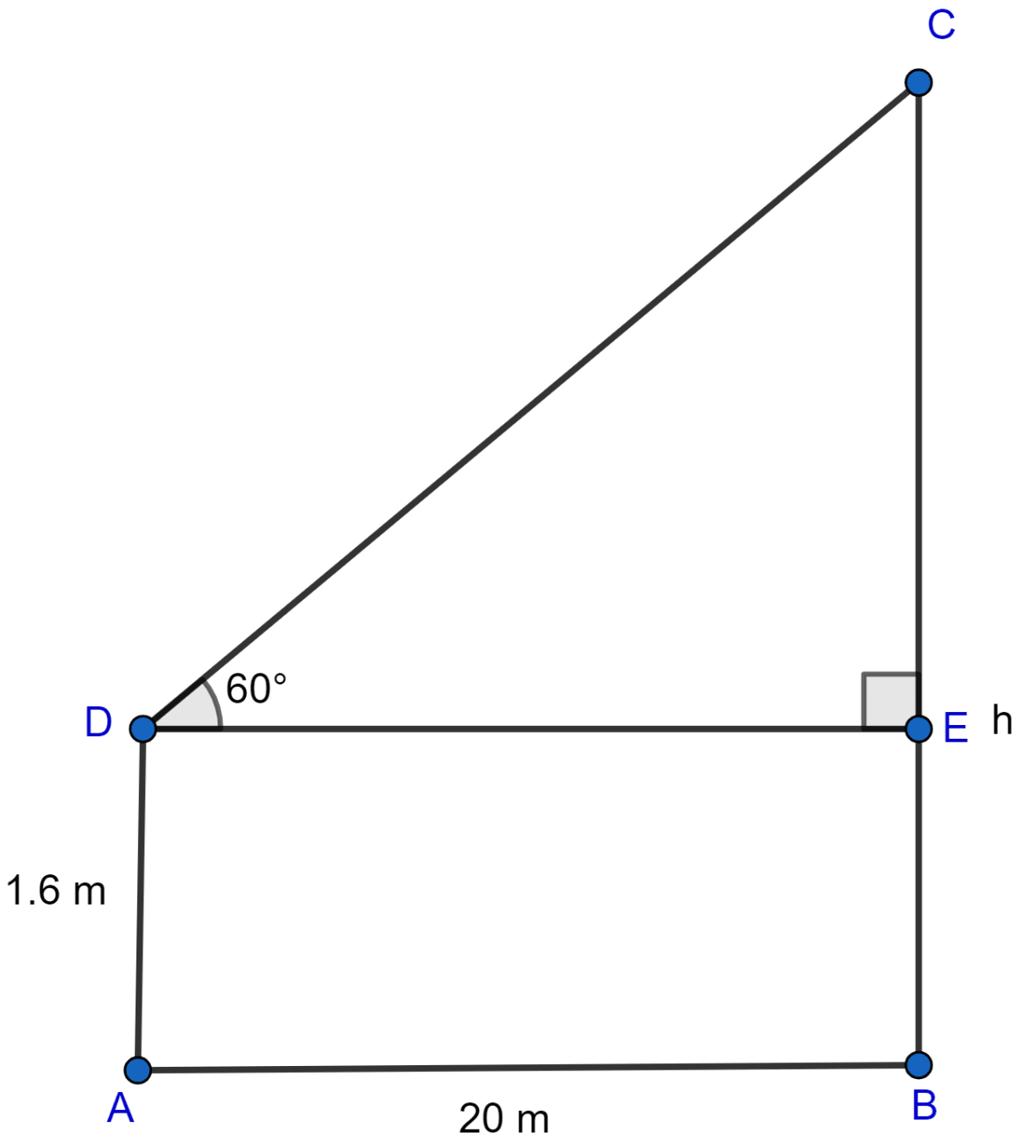
A boy, 1.6 m tall, is 20 m away from a tower and observes that the angle of elevation of the top of the tower is 60. Find the height of the tower. Heights and Distances, ML Aggarwal Understanding Mathematics Solutions ICSE Class 10.

From figure,

ABED is a rectangle.

BE = AD = 1.6 m
DE = AB = 20 m.

CE = BC - BE = (h - 1.6) m.

Considering right angled triangle △DCE,

⇒tan 60°=CEDE⇒3=h−1.620⇒h−1.6=203⇒h−1.6=34.64⇒h=36.24 m.\Rightarrow \text{tan 60°} = \dfrac{CE}{DE} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h - 1.6}{20} \\[1em] \Rightarrow h - 1.6 = 20\sqrt{3} \\[1em] \Rightarrow h - 1.6 = 34.64 \\[1em] \Rightarrow h = 36.24 \text{ m}.

Hence, the height of tower is 36.24 m.

Answered By

10 Likes

Related Questions