The angle of elevation of the top of a tower from a point A (on the ground) is 30°. On walking 50 m towards the tower, the angle of elevation is found to be 60°. Calculate :

(i) the height of the tower (correct to one decimal place)

(ii) the distance of the tower from A.

Consider the below figure:

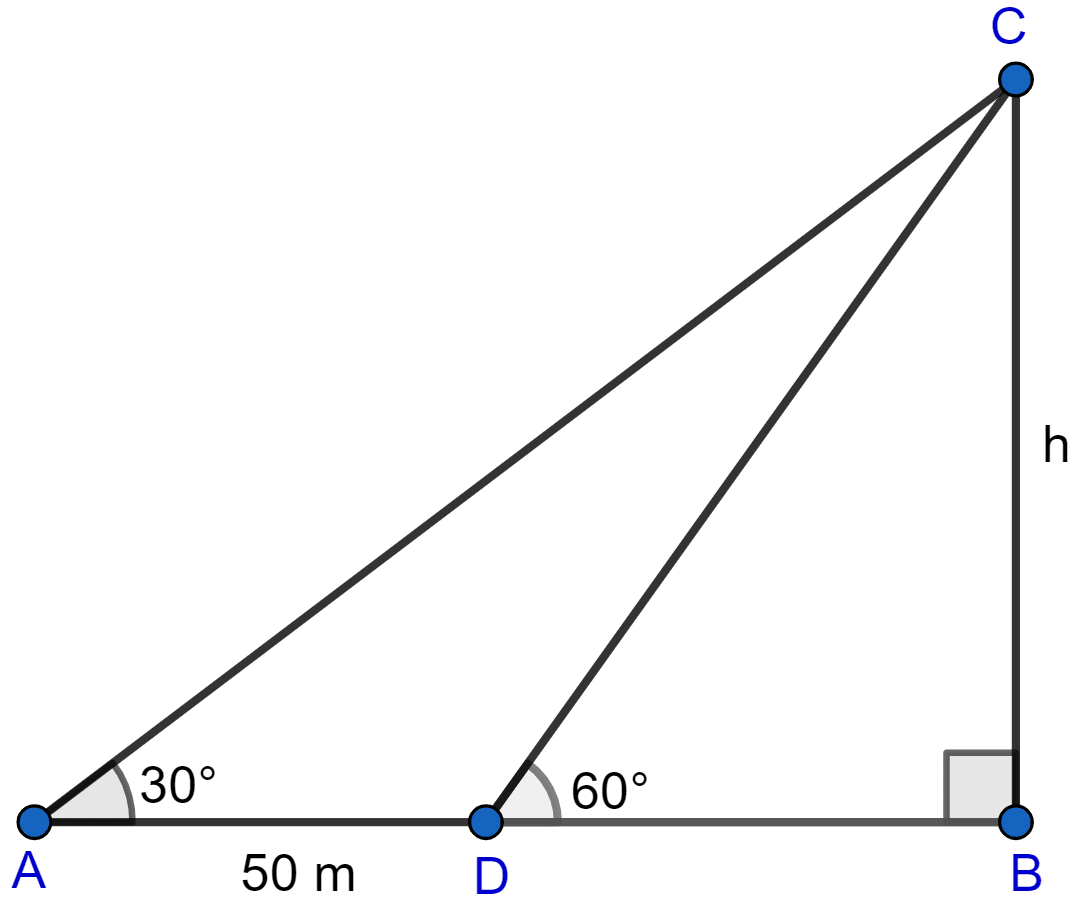
(i) Let after moving 50 m towards tower from point A, the person reaches point D and height of tower be h meters.

From figure,

AD = 50 m, AB = AD + DB = (50 + DB) m

Considering right angled triangle △ABC,

$\Rightarrow \text{tan 30°} = \dfrac{BC}{AB} \\[1em] \Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{h}{50 + DB} \\[1em] \Rightarrow 50 + DB = h\sqrt{3} \text{ …….( Eq 1)}$

Considering right angled triangle △BCD,

$\Rightarrow \text{tan 60°} = \dfrac{BC}{DB} \\[1em] \Rightarrow \sqrt{3} = \dfrac{h}{DB} \\[1em] \Rightarrow h = DB\sqrt{3} \text{ …….( Eq 2)}$

Putting value of h from Eq 2 in Eq 1 we get,

$\Rightarrow 50 + DB = DB\sqrt{3} \times \sqrt{3} \\[1em] \Rightarrow 50 + DB = 3DB \\[1em] \Rightarrow 2DB = 50 \\[1em] \Rightarrow DB = 25 \\[1em] \therefore h = DB\sqrt{3} = 25 \times 1.732 = 43.3 \text{ m}$

Hence, the height of tower is 43.3 m.

(ii) From figure,

Distance of tower from A (AB) = AD + DB = 50 + 25 = 75 m.

Hence, the distance of tower from A is 75 m.