Triangles

Fill in the blanks using the correct word given in brackets :

(i) All circles are ............... (congruent, similar)

(ii) All squares are ............... (similar, congruent)

(iii) All ............... triangles are similar. (isosceles, equilateral)

(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are ............... and (b) their corresponding sides are ............... . (equal, proportional)

Answer

(i) Similar

(ii) Similar

(iii) Equilateral

(iv) Equal, Proportion.

Give two different examples of pair of

(i) similar figures.

(ii) non-similar figures.

Answer

(i) Two examples of pair of similar figures are :

Two equilateral triangles of sides 2 cm and 6 cm.

(ii) Two examples of pair of non-similar figures are :

A quadrilateral and a rectangle.

State whether the following quadrilaterals are similar or not :

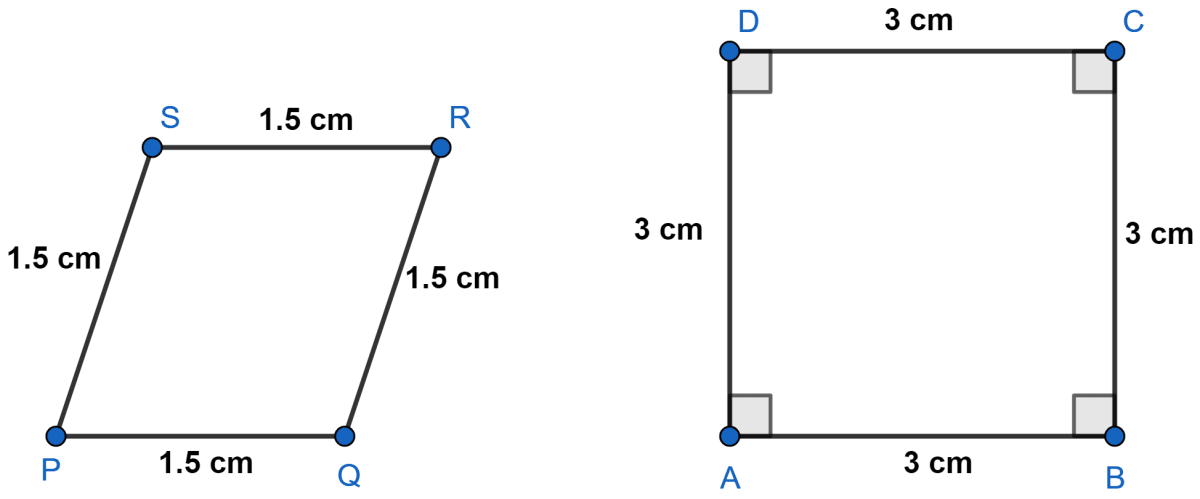
Answer

Two polygons of the same number of sides are similar if

1. All the corresponding angles are equal.
2. All the corresponding sides are in the same ratio (or proportion).

In quadrilaterals ABCD and PQRS,

⇒ $\dfrac{AB}{PQ} = \dfrac{3}{1.5} = \dfrac{30}{15}$ = 2,

⇒ $\dfrac{BC}{QR} = \dfrac{3}{1.5} = \dfrac{30}{15}$ = 2,

⇒ $\dfrac{CD}{RS} = \dfrac{3}{1.5} = \dfrac{30}{15}$ = 2,

⇒ $\dfrac{AD}{SP} = \dfrac{3}{1.5} = \dfrac{30}{15}$ = 2.

So,

$\Rightarrow \dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{CD}{RS} = \dfrac{AD}{SP}$.

⇒ Corresponding sides are in proportion.

But ∠A ≠ ∠P; ∠B ≠ ∠Q

Thus, corresponding angles are not equal.

Hence, quadrilateral ABCD is not similar to quadrilateral PQRS.

In figure, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

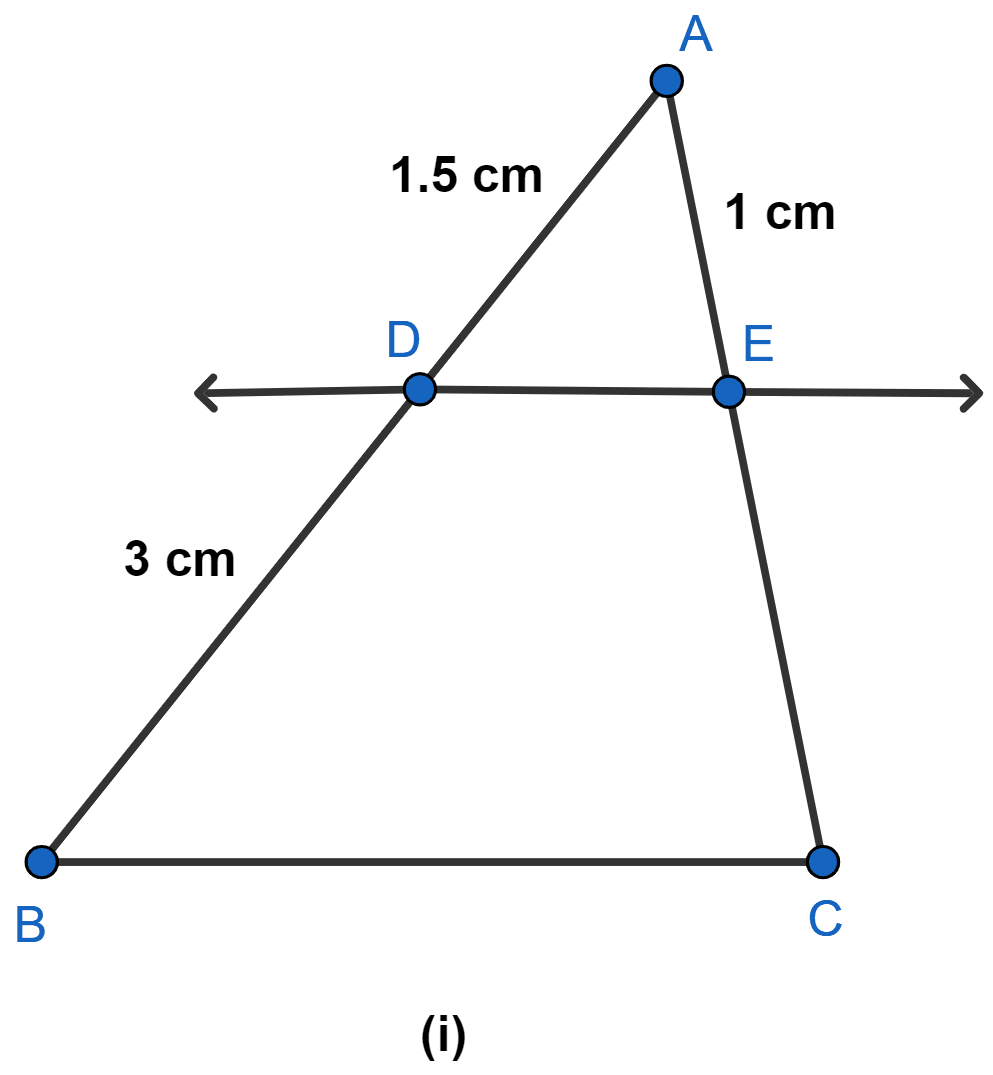
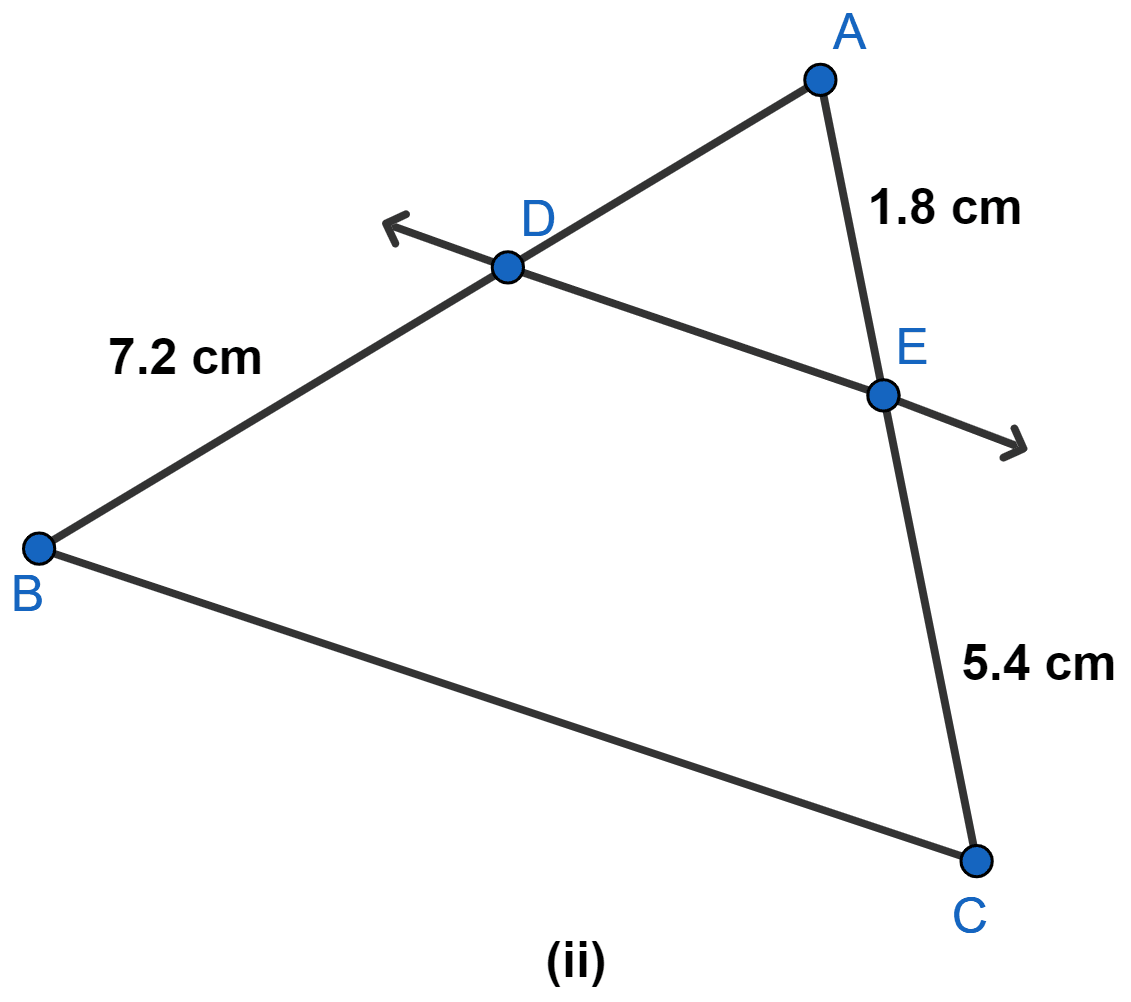
Answer

(i) We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

$\therefore \dfrac{AD}{BD} = \dfrac{AE}{EC} \\[1em] \Rightarrow \dfrac{1.5}{3}= \dfrac{1}{EC} \\[1em] \Rightarrow EC = \dfrac{3 \times 1}{1.5} \\[1em] \Rightarrow EC = 2 \text{ cm}.$

Hence, EC = 2 cm.

(ii) We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

$\therefore \dfrac{AD}{BD} = \dfrac{AE}{EC} \\[1em] \Rightarrow \dfrac{AD}{7.2}= \dfrac{1.8}{5.4} \\[1em] \Rightarrow \dfrac{AD}{7.2} = \dfrac{1}{3} \\[1em] \Rightarrow AD = 7.2 \times \dfrac{1}{3} = 2.4 \text{ cm}.$

Hence, AD = 2.4 cm.

E and F are points on the sides PQ and PR respectively of a △PQR. For each of the following cases, state whether EF || QR :

(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

Answer

We know that,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

∴ EF || QR if

$\dfrac{PE}{EQ} = \dfrac{PF}{FR}$ ...........(1)

(i) Given,

PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm.

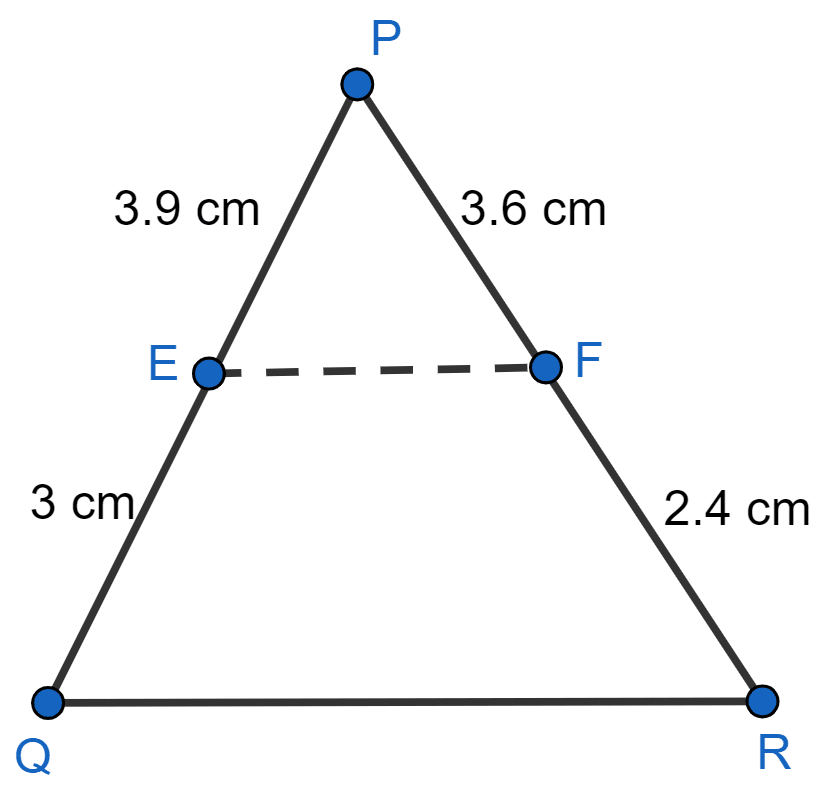
Substituting values in L.H.S. of equation (1), we get :

$\Rightarrow \dfrac{PE}{EQ} = \dfrac{3.9}{3} \\[1em] = \dfrac{1.3}{1} \\[1em] = \dfrac{13}{10}.$

Substituting values in R.H.S. of equation (1), we get :

$\Rightarrow \dfrac{PF}{FR} = \dfrac{3.6}{2.4} \\[1em] = \dfrac{36}{24} \\[1em] = \dfrac{3}{2}.$

Since, $\dfrac{PE}{EQ} \ne \dfrac{PF}{FR}$.

Hence, in this case EF is not parallel to QR.

(ii) Given,

PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm.

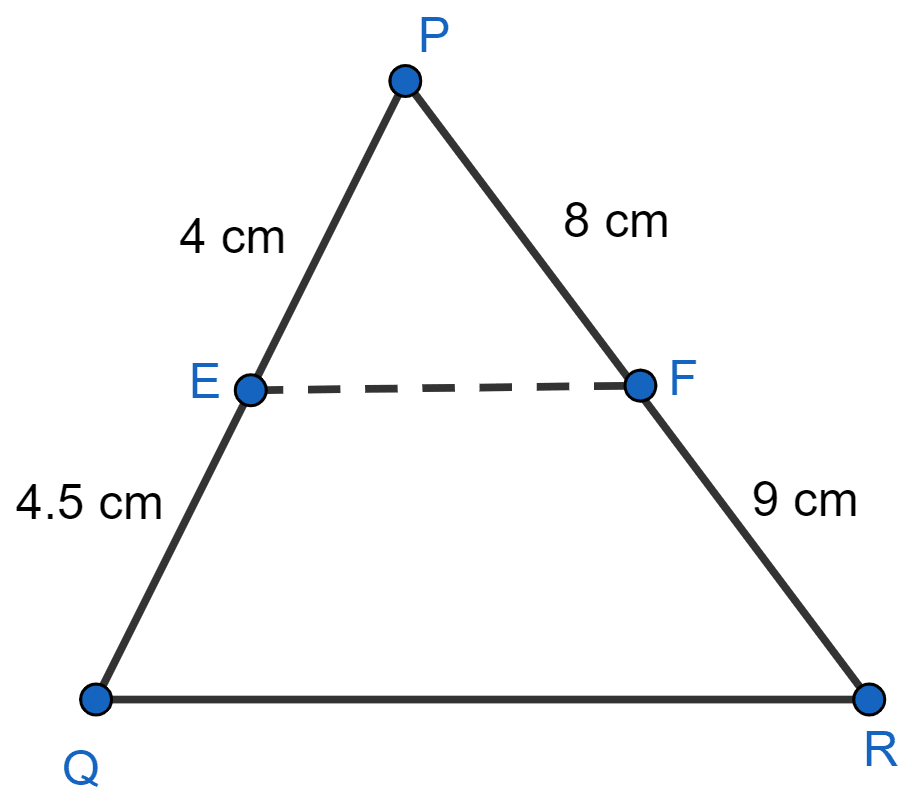
Substituting values in L.H.S. of equation (1), we get :

$\Rightarrow \dfrac{PE}{EQ} = \dfrac{4}{4.5} \\[1em] = \dfrac{40}{45} \\[1em] = \dfrac{8}{9}.$

Substituting values in R.H.S. of equation (1), we get :

$\Rightarrow \dfrac{PF}{FR} = \dfrac{8}{9}$

Since, $\dfrac{PE}{EQ} = \dfrac{PF}{FR}$.

Hence, in this case EF is parallel to QR.

(iii) Given,

PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.

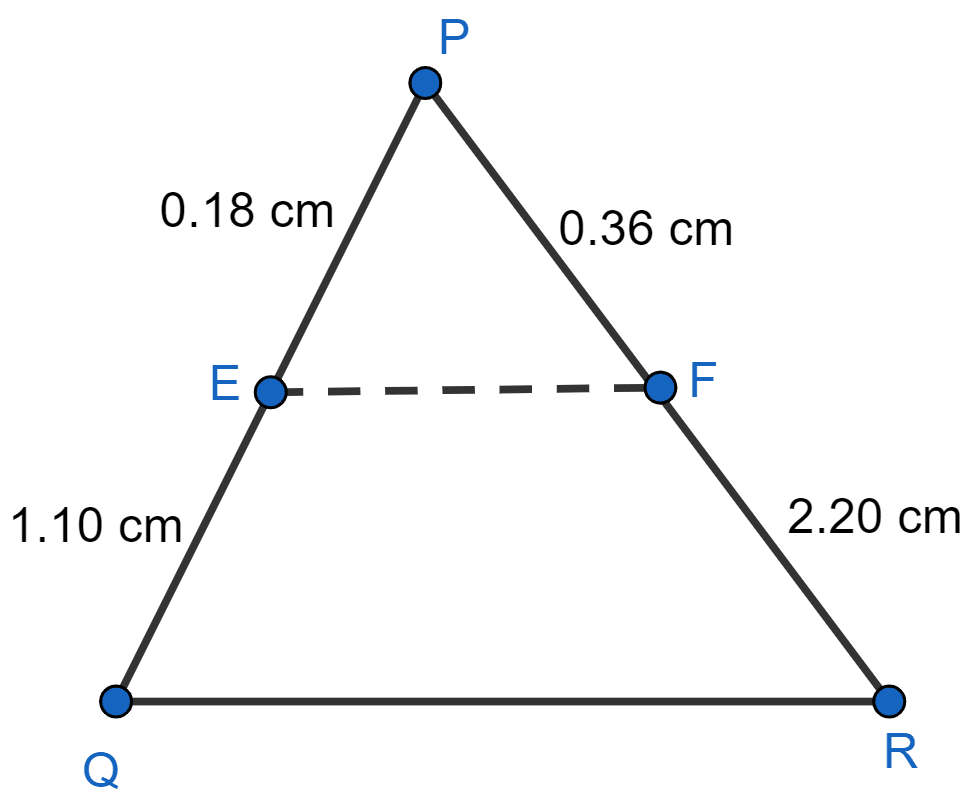
From figure,

⇒ EQ = PQ - PE = 1.28 - 0.18 = 1.10 cm

⇒ FR = PR - PF = 2.56 - 0.36 = 2.20 cm

Substituting values in L.H.S. of equation (1), we get :

$\Rightarrow \dfrac{PE}{EQ} = \dfrac{0.18}{1.10} \\[1em] = \dfrac{18}{110} \\[1em] = \dfrac{9}{55}.$

Substituting values in R.H.S. of equation (1), we get :

$\Rightarrow \dfrac{PF}{FR} = \dfrac{0.36}{2.20} \\[1em] = \dfrac{36}{220} \\[1em] = \dfrac{9}{55}.$

Since, $\dfrac{PE}{EQ} = \dfrac{PF}{FR}$.

Hence, in this case EF is parallel to QR.

In figure, if LM || CB and LN || CD, prove that

$\dfrac{AM}{AB} = \dfrac{AN}{AD}$.

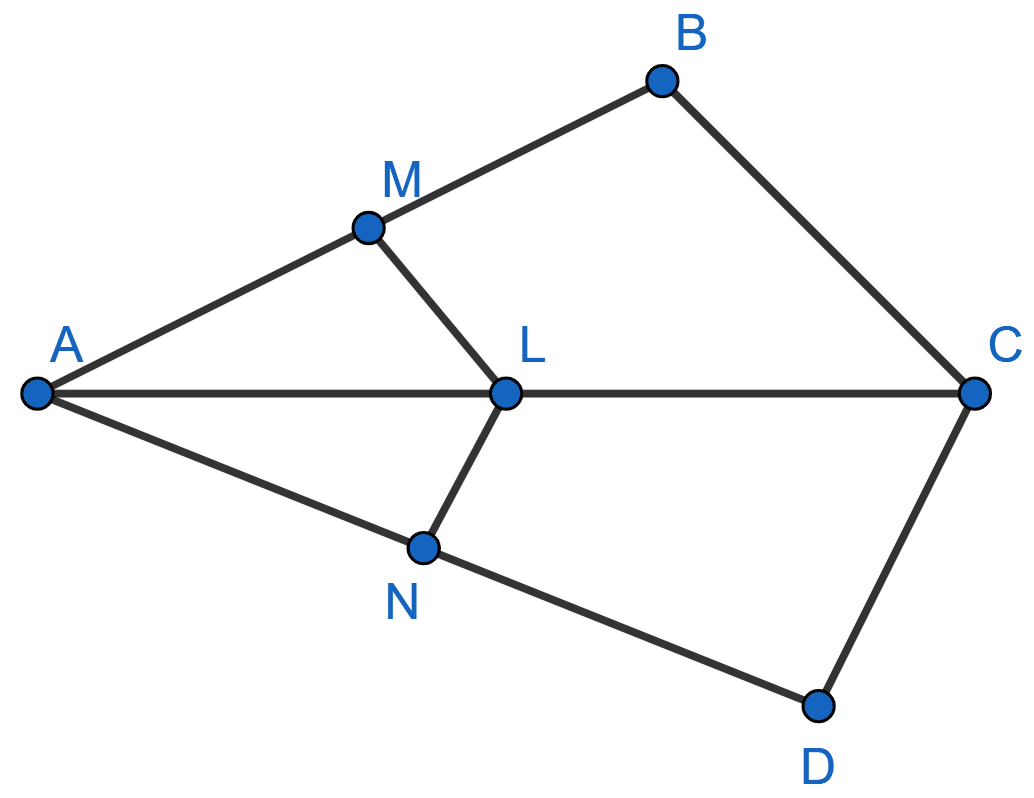
Answer

We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

In Δ ABC,

LM || CB [∵ Given]

$\therefore \dfrac{AM}{MB} = \dfrac{AL}{LC}$ ............ (1)

In Δ ACD,

LN || CD [∵ Given]

$\therefore \dfrac{AN}{DN} = \dfrac{AL}{LC}$ ............ (2)

From equations (1) and (2),

$\Rightarrow \dfrac{AM}{MB} = \dfrac{AN}{DN} \\[1em] \Rightarrow \dfrac{MB}{AM} = \dfrac{DN}{AN}$

Adding 1 on both sides, we get :

$\Rightarrow \dfrac{MB}{AM} + 1 = \dfrac{DN}{AN} + 1 \\[1em] \Rightarrow \dfrac{(MB + AM)}{AM} = \dfrac{(DN + AN)}{AN} \\[1em] \Rightarrow \dfrac{AB}{AM} = \dfrac{AD}{AN} \\[1em] \Rightarrow \dfrac{AM}{AB} = \dfrac{AN}{AD}.$

Hence, proved that $\dfrac{AM}{AB} = \dfrac{AN}{AD}.$.

In figure, DE || AC and DF || AE. Prove that $\dfrac{BF}{FE} = \dfrac{BE}{EC}$.

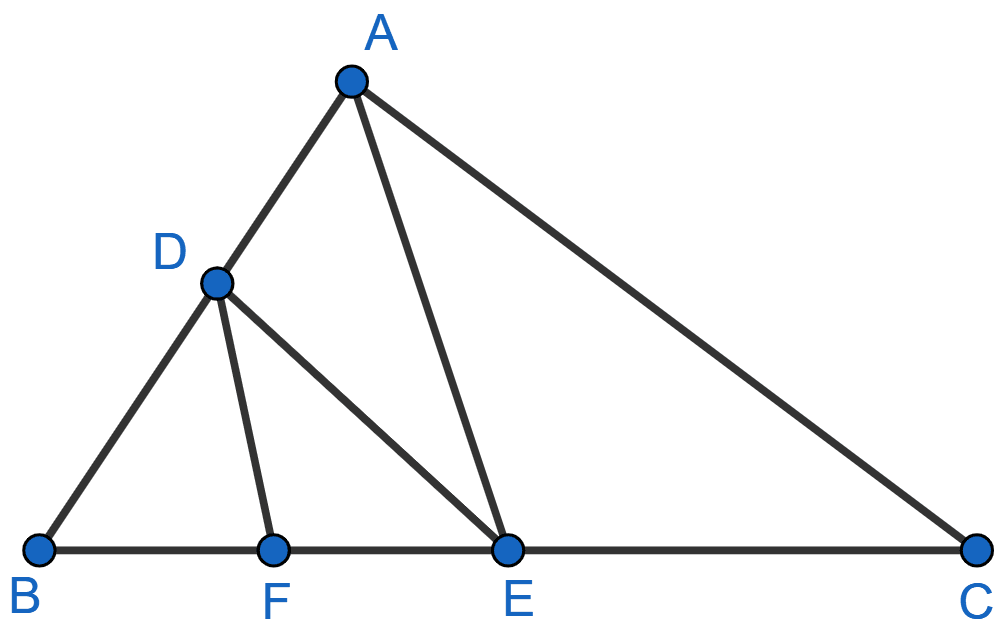
Answer

We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points, the other two sides are divided in the same ratio.

In Δ ABC,

DE || AC [∵ Given]

$\therefore \dfrac{BD}{AD} = \dfrac{BE}{EC}$ .........(1)

In Δ ABE,

DF || AE [∵ Given]

$\therefore \dfrac{BD}{AD} = \dfrac{BF}{FE}$ ........(2)

From (1) and (2), we get :

$\Rightarrow \dfrac{BE}{EC} = \dfrac{BF}{FE}$

Hence, proved that $\dfrac{BF}{FE} = \dfrac{BE}{EC}$.

In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.

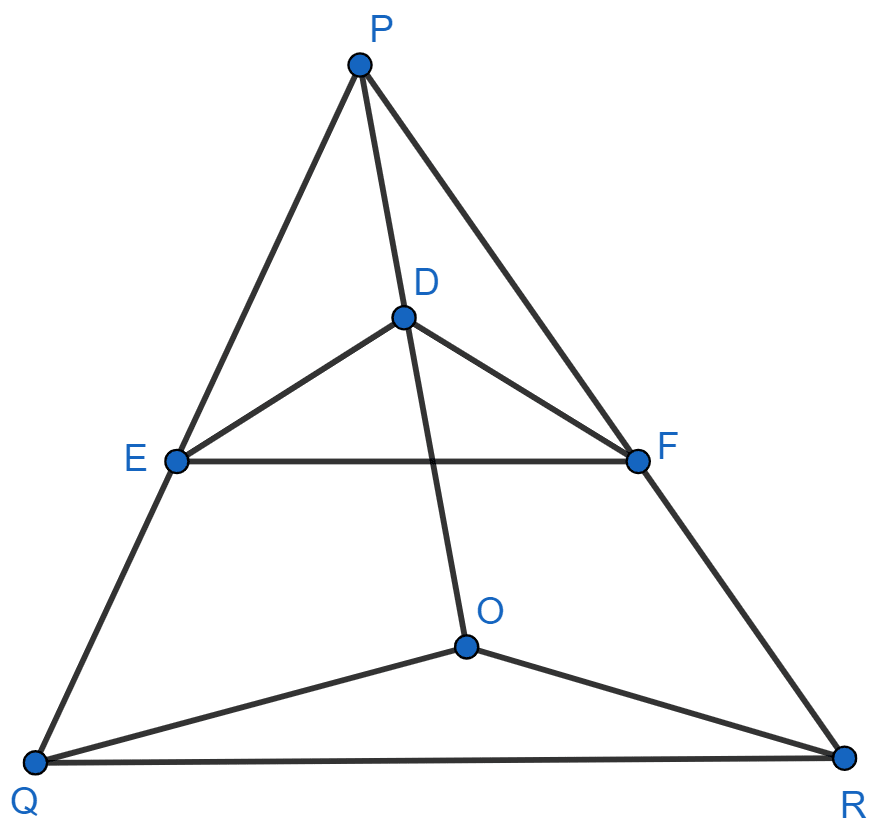
Answer

We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points, the other two sides are divided in the same ratio.

In Δ POQ,

DE || OQ [∵ Given]

$\therefore \dfrac{PE}{EQ} = \dfrac{PD}{DO}$ ..........(1)

In Δ POR,

DF || OR [∵ Given]

$\dfrac{PF}{FR} = \dfrac{PD}{DO}$ ......... (2)

From equation (1) and (2), we get :

$\Rightarrow \dfrac{PE}{EQ} = \dfrac{PF}{FR}$

In Δ PQR,

$\Rightarrow \dfrac{PE}{EQ} = \dfrac{PF}{FR}$

We know that,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

∴ EF || QR.

Hence, proved that EF || QR.

In figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

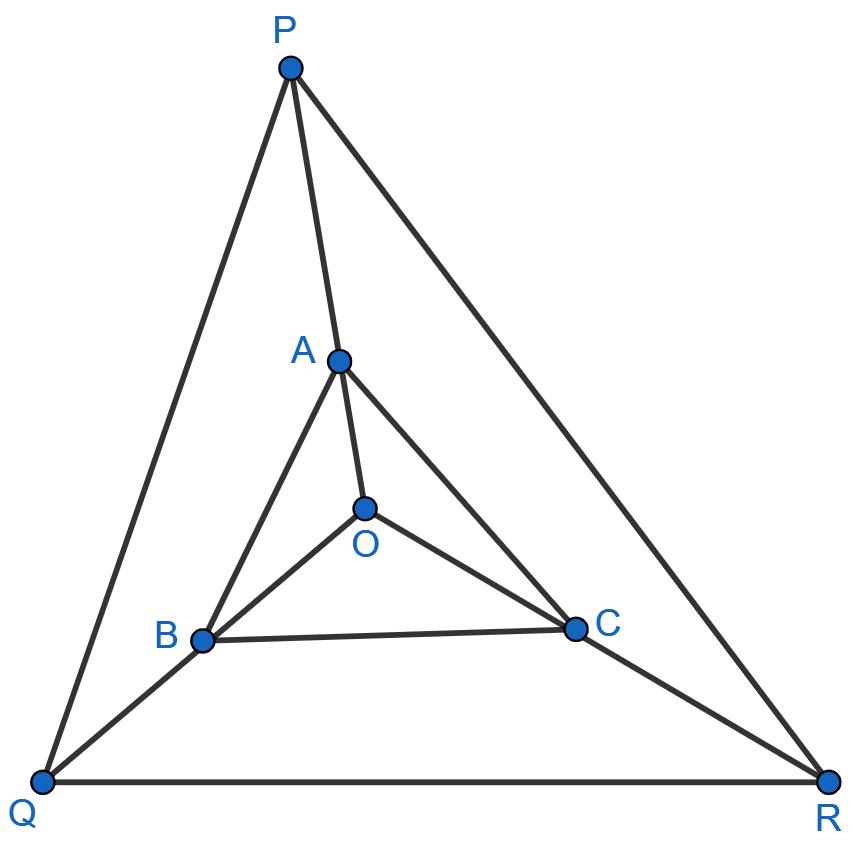
Answer

We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points, the other two sides are divided in the same ratio.

In Δ OPQ,

AB || PQ [∵ Given]

$\therefore \dfrac{OA}{AP} = \dfrac{OB}{BQ}$ .............. (1)

In Δ OPR,

AC || PR [∵ Given]

$\dfrac{OA}{AP} = \dfrac{OC}{CR}$ ............. (2)

From equations (1) and (2), we get :

$\dfrac{OB}{BQ} = \dfrac{OC}{CR}$

In Δ OQR,

$\Rightarrow \dfrac{OB}{BQ} = \dfrac{OC}{CR}$.

We know that,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

∴ BC || QR.

Hence, proved that BC || QR.

Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.

Answer

Let ABC be the triangle and D be the mid-point of AB and DE || BC.

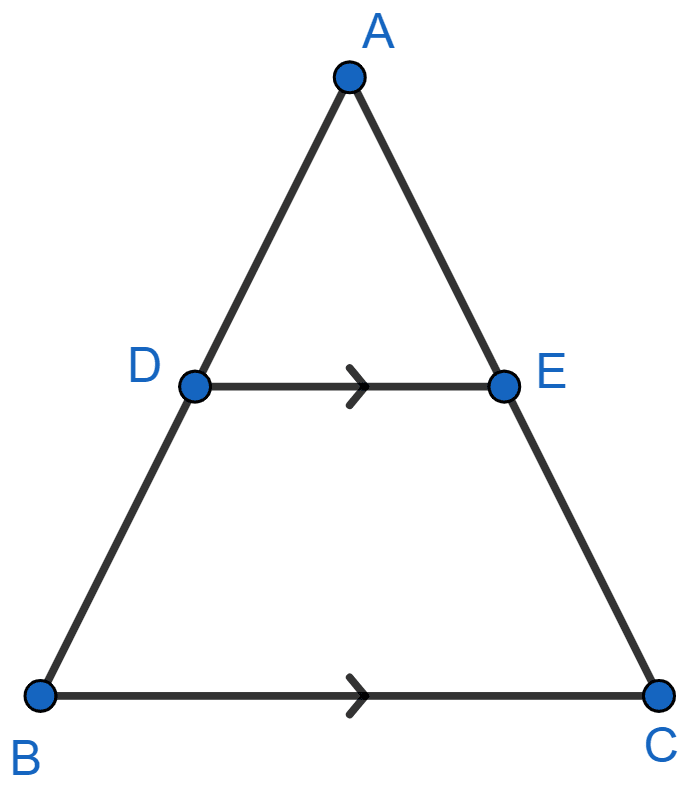
By theorem 6.1,

If a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points, the other two sides are divided in the same ratio.

So, In △ ABC,

$\therefore \dfrac{AD}{BD} = \dfrac{AE}{EC} \\[1em] \Rightarrow \dfrac{AE}{EC} = 1 \text{ (Since, D is the mid-point of AB so, AD = BD.)}\\[1em] \Rightarrow AE = EC.$

Since, AE = EC.

∴ E bisects AC.

Hence, proved that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.

Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.

Answer

Let ABC be the triangle, D be the mid-point AB and E be the mid-point of AC.

So, in △ ABC,

$\dfrac{AD}{BD} = 1$ .........(1)

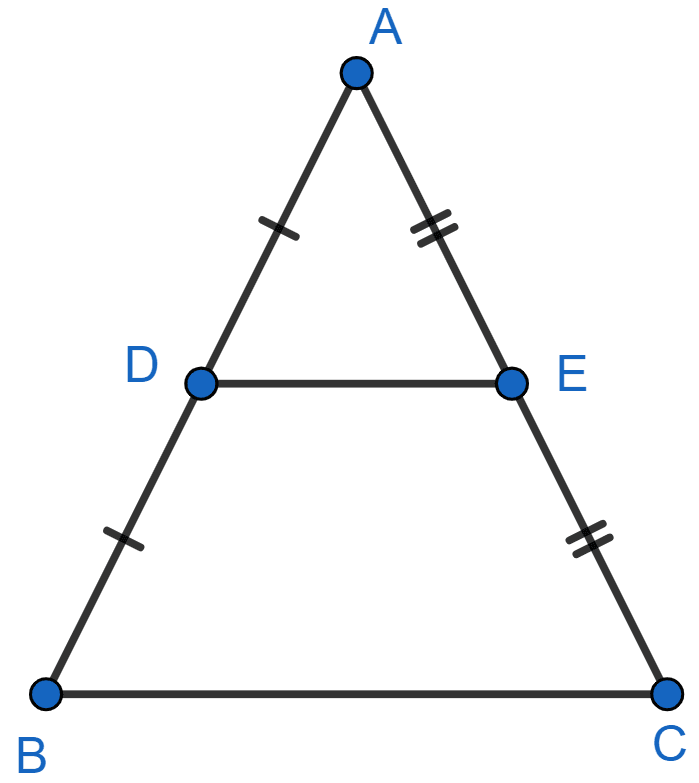
$\dfrac{AE}{EC} = 1$ .........(2)

From (1) and (2), we get :

$\therefore \dfrac{AD}{BD} = \dfrac{AE}{EC}$.

By theorem 6.2,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

Since, In △ ABC,

$\dfrac{AD}{BD} = \dfrac{AE}{EC}$.

∴ DE || BC.

Hence, proved that the line joining the mid-points of any two sides of a triangle is parallel to the third side.

ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that $\dfrac{AO}{BO} = \dfrac{CO}{DO}$.

Answer

Given,

ABCD is a trapezium in which AB || DC and its diagonals AC and BD intersect each other at O.

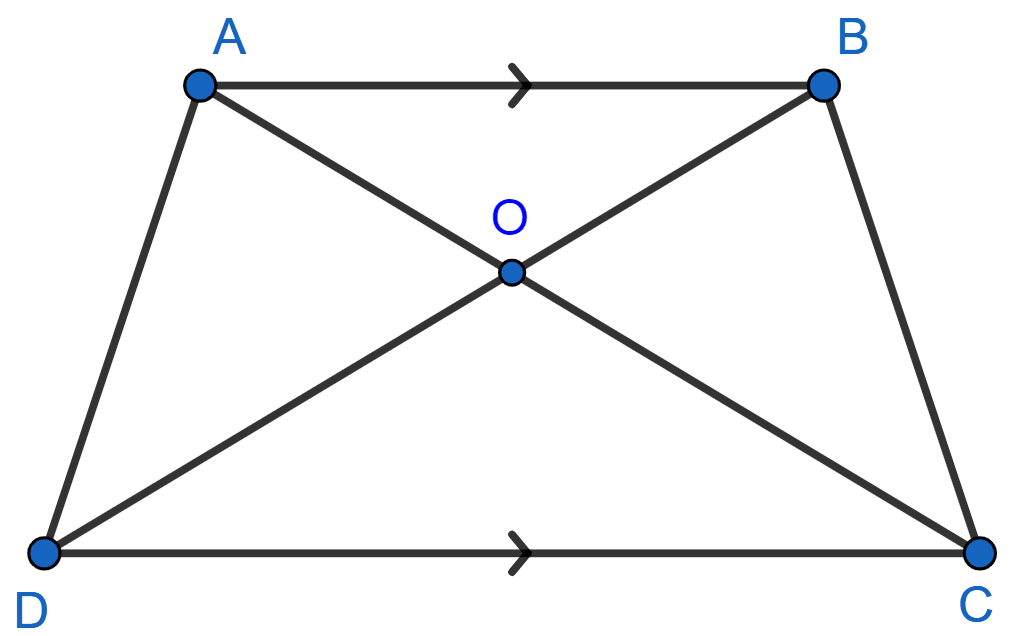
We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides at distinct points, the other two sides are divided in the same ratio.

Through O, draw EO || DC || AB.

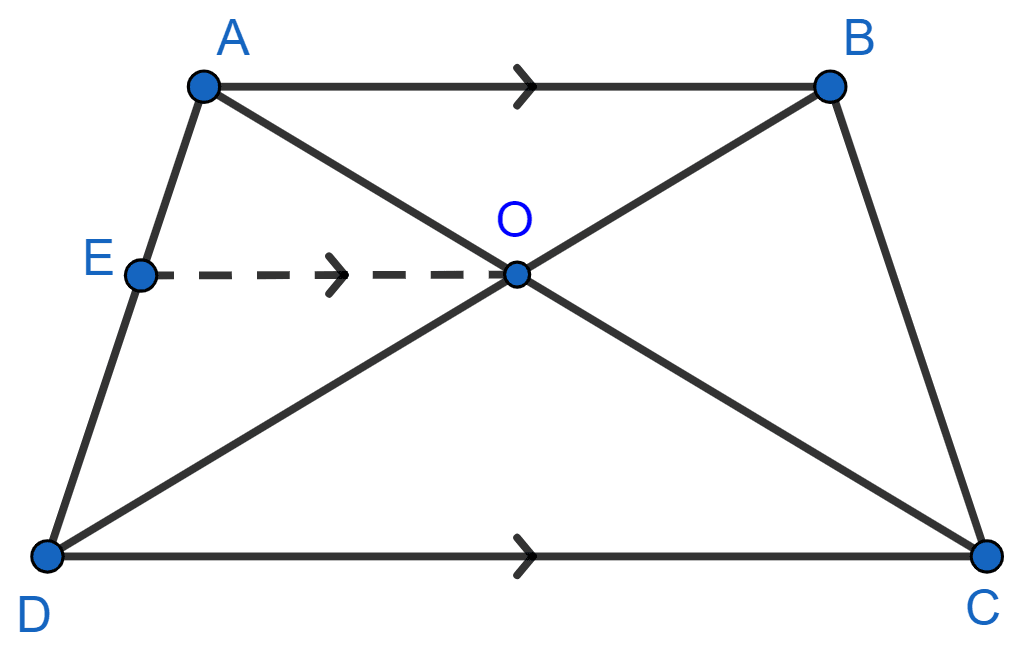
In △ ADC,

OE || DC

$\therefore \dfrac{AE}{ED} = \dfrac{AO}{CO}$ ......(1)

In △ ABD,

OE || AB

$\therefore \dfrac{AE}{ED} = \dfrac{BO}{DO}$ ......(2)

From (1) and (2), we get :

$\Rightarrow \dfrac{AO}{CO} = \dfrac{BO}{DO} \\[1em] \Rightarrow \dfrac{AO}{BO} = \dfrac{CO}{DO}.$

Hence, proved that $\dfrac{AO}{BO} = \dfrac{CO}{DO}.$

The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\dfrac{AO}{BO} = \dfrac{CO}{DO}.$ Show that ABCD is a trapezium.

Answer

Let ABCD be the quadrilateral where AC and BD intersect each other at O such that $\dfrac{AO}{BO} = \dfrac{CO}{DO}$.

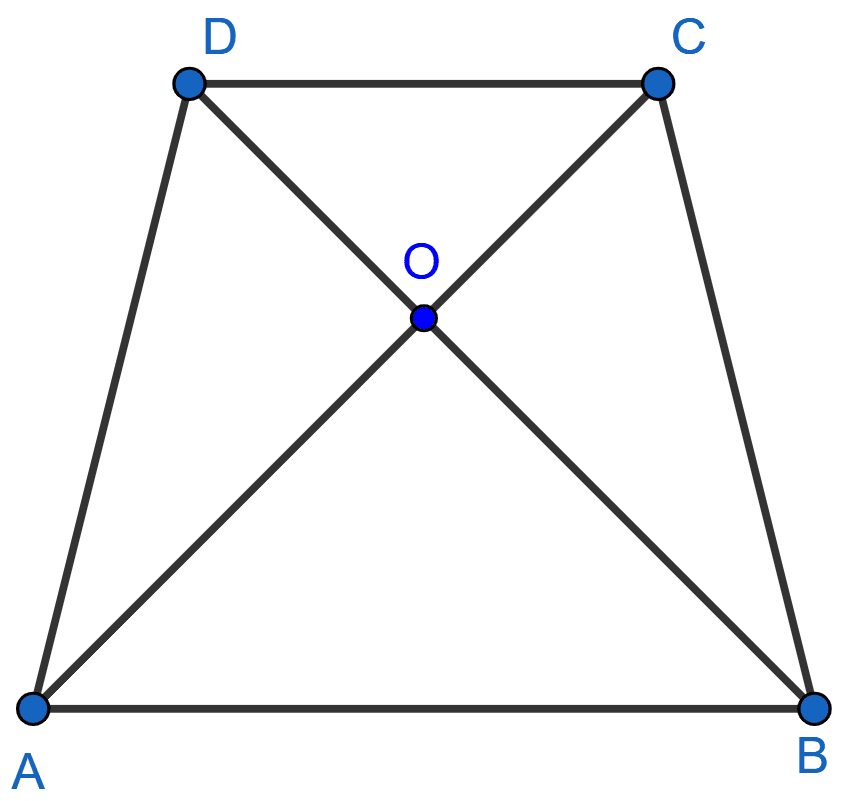
From point O,

Draw a line EO touching AD at E in such a way that, EO || AB.

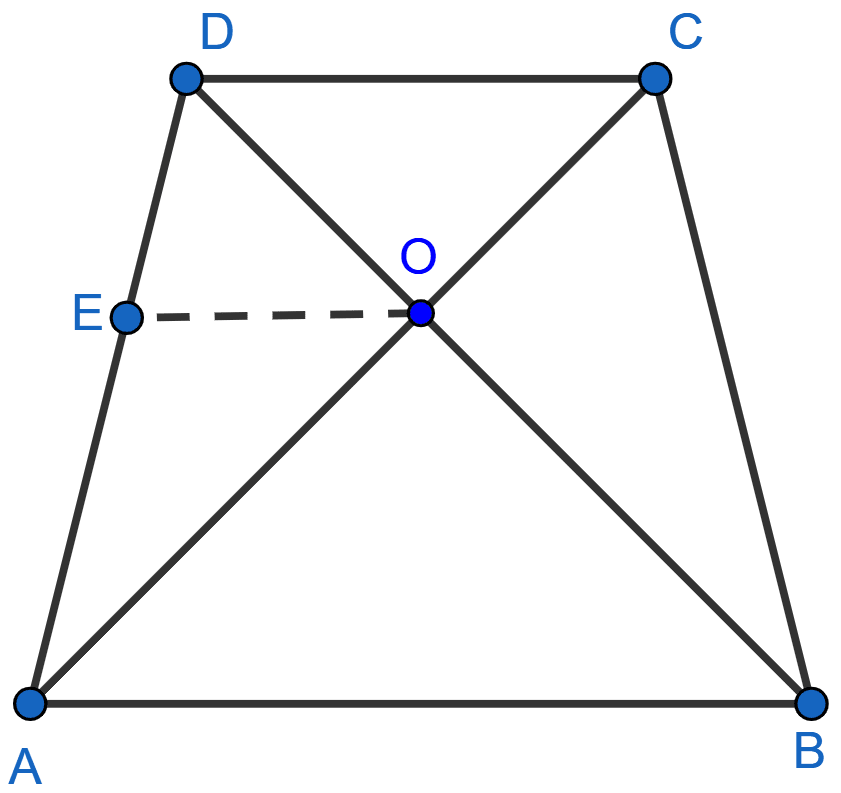
We know that,

If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

In △ DAB,

EO || AB

$\therefore \dfrac{DE}{EA} = \dfrac{DO}{OB}$ ..........(1)

Given,

$\Rightarrow \dfrac{AO}{BO} = \dfrac{CO}{DO} \\[1em] \Rightarrow \dfrac{AO}{CO} = \dfrac{BO}{DO} \\[1em] \Rightarrow \dfrac{CO}{AO} = \dfrac{DO}{BO} \text{ .........(2)}$

From (1) and (2), we get :

$\Rightarrow \dfrac{DE}{EA} = \dfrac{CO}{AO}$

We know that,

If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

∴ EO || DC.

Since, EO || AB and EO || DC.

∴ AB || DC.

Hence, proved that ABCD is a trapezium.

State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

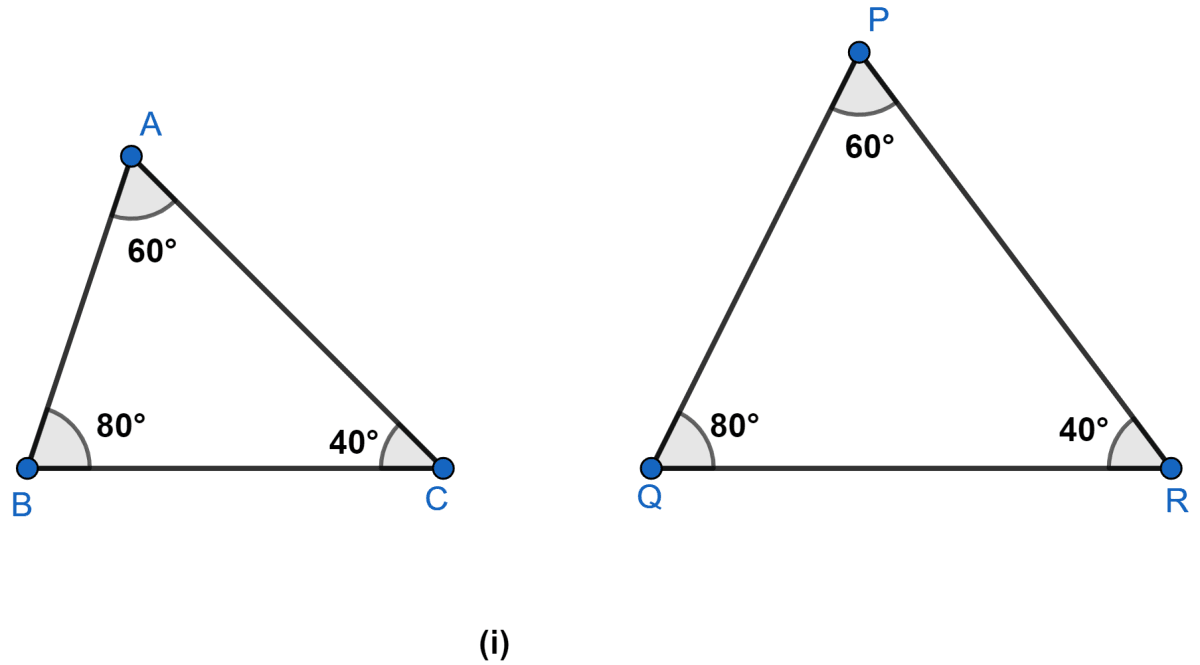
Answer

In Δ ABC and Δ PQR,

∠A = ∠P = 60°

∠B = ∠Q = 80°

∠C = ∠R = 40°

Hence, Δ ABC ~ Δ PQR by A.A.A. axiom.

State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

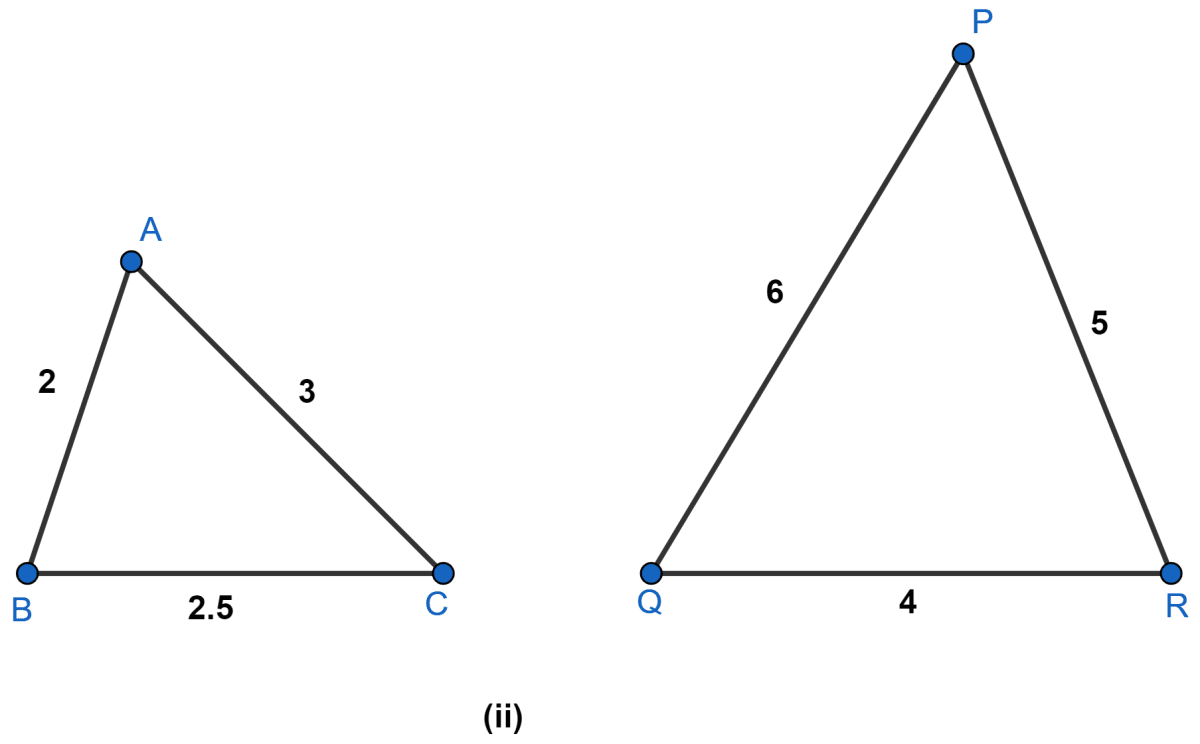
Answer

In Δ ABC and Δ PQR,

$\dfrac{AB}{QR} = \dfrac{2}{4} = \dfrac{1}{2}$

$\dfrac{BC}{PR} = \dfrac{2.5}{5} = \dfrac{1}{2}$

$\dfrac{AC}{PQ} = \dfrac{3}{6} = \dfrac{1}{2}$

Since,

$\Rightarrow \dfrac{AB}{QR} = \dfrac{BC}{PR} = \dfrac{AC}{PQ} = \dfrac{1}{2}$.

Hence, Δ ABC ~ Δ PQR by S.S.S. axiom.

State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

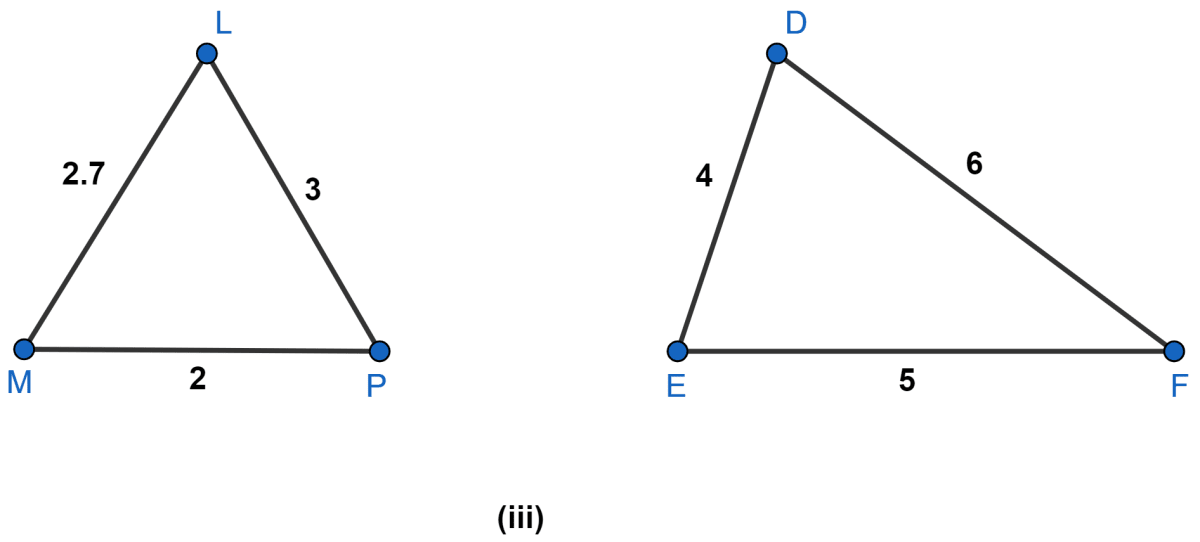
Answer

In Δ LMP and Δ FED

$\dfrac{LM}{FE} = \dfrac{2.7}{5} = \dfrac{27}{50}$

$\dfrac{MP}{ED} = \dfrac{2}{4} = \dfrac{1}{2}$

$\dfrac{LP}{FD} = \dfrac{3}{6} = \dfrac{1}{2}$

All the corresponding sides of the two triangles are not in the same proportion.

Hence triangles are not similar.

State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

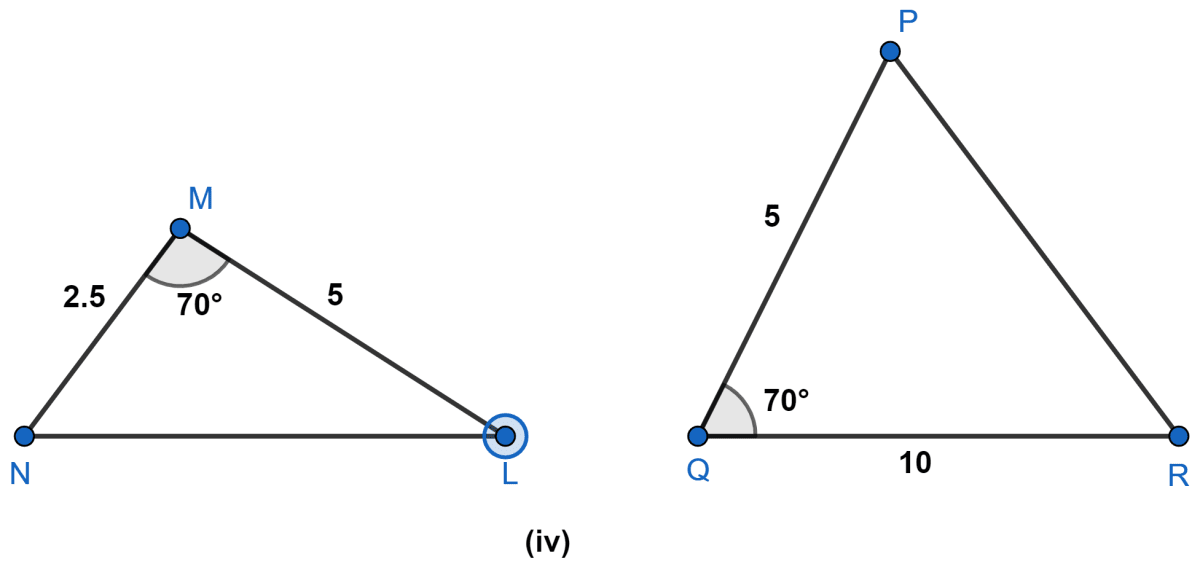
Answer

In ΔMNL and ΔQPR,

$\Rightarrow \dfrac{NM}{PQ} = \dfrac{2.5}{5} = \dfrac{1}{2}$

$\Rightarrow \dfrac{ML}{QR} = \dfrac{5}{10} = \dfrac{1}{2}$

$\therefore \dfrac{NM}{PQ} = \dfrac{ML}{QR} = \dfrac{1}{2}$.

∠M = ∠Q = 70°.

Hence, ΔMNL ~ ΔQPR by S.A.S. axiom.

State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

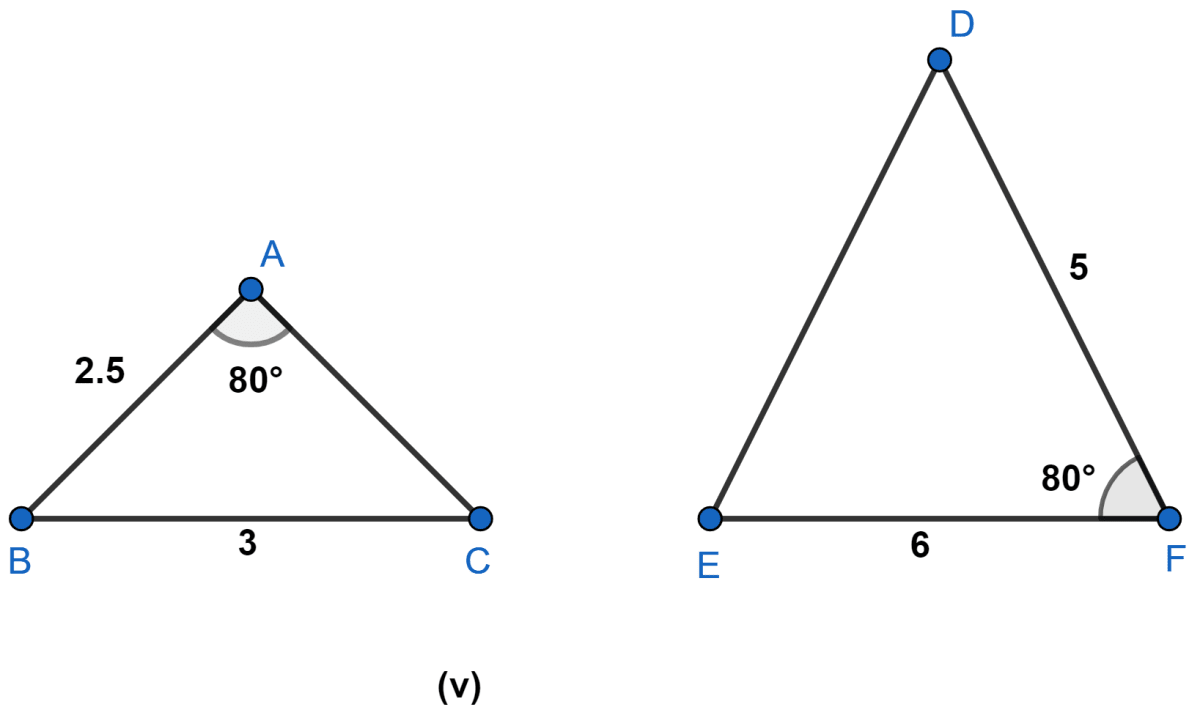
Answer

In Δ ABC and Δ DFE,

$\dfrac{AB}{DF} = \dfrac{2.5}{5} = \dfrac{1}{2}$

$\dfrac{BC}{EF} = \dfrac{3}{6} = \dfrac{1}{2}$

$\therefore \dfrac{AB}{DF} = \dfrac{BC}{EF} = \dfrac{1}{2}$

∠A = ∠F.

∠B must be equal to 80° as the sides AB, BC includes ∠B , not ∠A.

Hence, the triangles are not similar

State which pairs of triangles are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

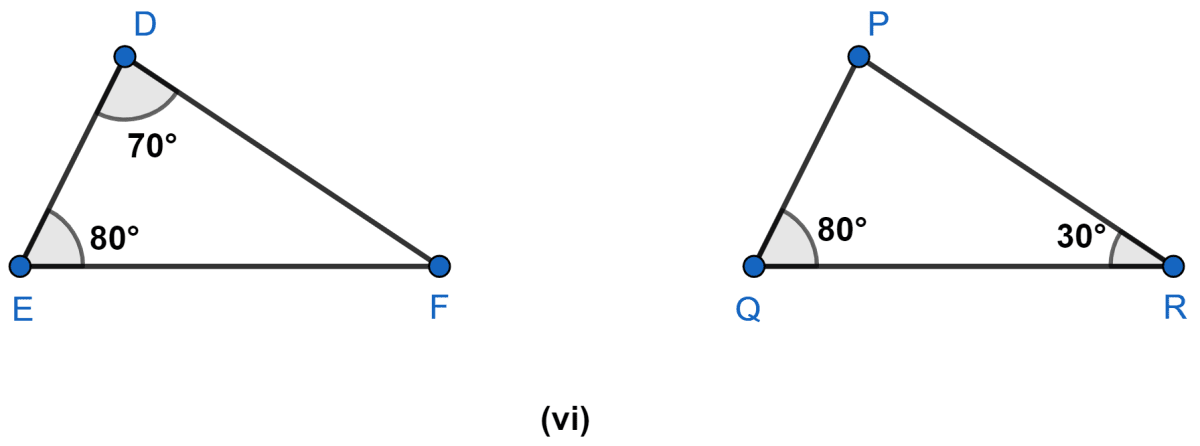
Answer

In Δ DEF,

∠D = 70°, ∠E = 80°

⇒ ∠D + ∠E + ∠F = 180° [By angle sum property of triangle]

⇒ 70° + 80° + ∠F = 180°

⇒ ∠F + 150° = 180°

⇒ ∠F = 180° - 150°

⇒ ∠F = 30°

In Δ PQR

∠Q = 80° , ∠R = 30°

⇒ ∠Q + ∠R + ∠P = 180° [By angle sum property pf triangle]

⇒ 80° + 30° + ∠P = 180°

⇒ ∠P + 110° = 180°

⇒ ∠P = 180° - 110°

⇒ ∠P = 70°.

In Δ DEF and Δ PQR,

⇒ ∠D = ∠P = 70°

⇒ ∠E = ∠Q = 80°

⇒ ∠F = ∠R = 30°

Hence, Δ DEF ~ Δ PQR by A.A.A. axiom.

In given figure, △ ODC ~ △ OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.

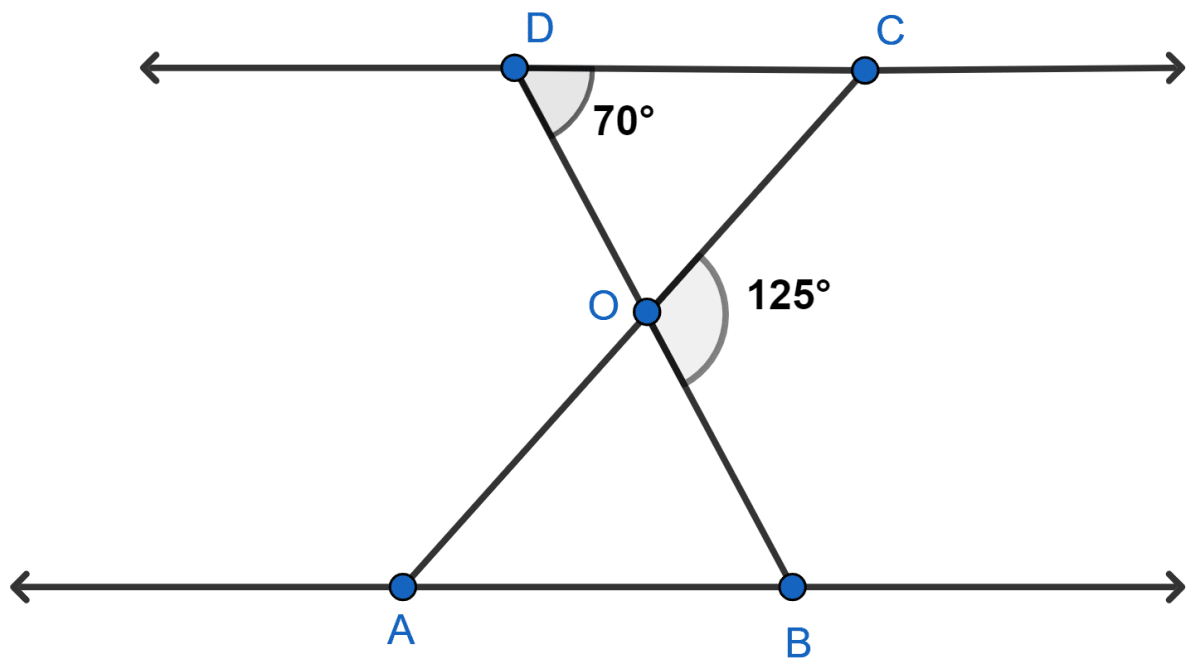
Answer

From figure,

DOB is a straight line. So, ∠DOC and ∠BOC forms a linear pair.

⇒ ∠DOC + ∠BOC = 180°

⇒ ∠DOC + 125° = 180°

⇒ ∠DOC = 180° - 125° = 55°.

In △DOC,

⇒ ∠DOC + ∠CDO + ∠DCO = 180° [By angle sum property of triangle]

⇒ 55° + 70° + ∠DCO = 180°

⇒ ∠DCO = 180° - 125° = 55°.

From figure,

⇒ ∠OAB = ∠DCO = 55°. [Alternate angles are equal]

Hence, ∠DOC = 55°, ∠DCO = 55°, ∠OAB = 55°.

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$.

Answer

Trapezium ABCD is shown in the figure below:

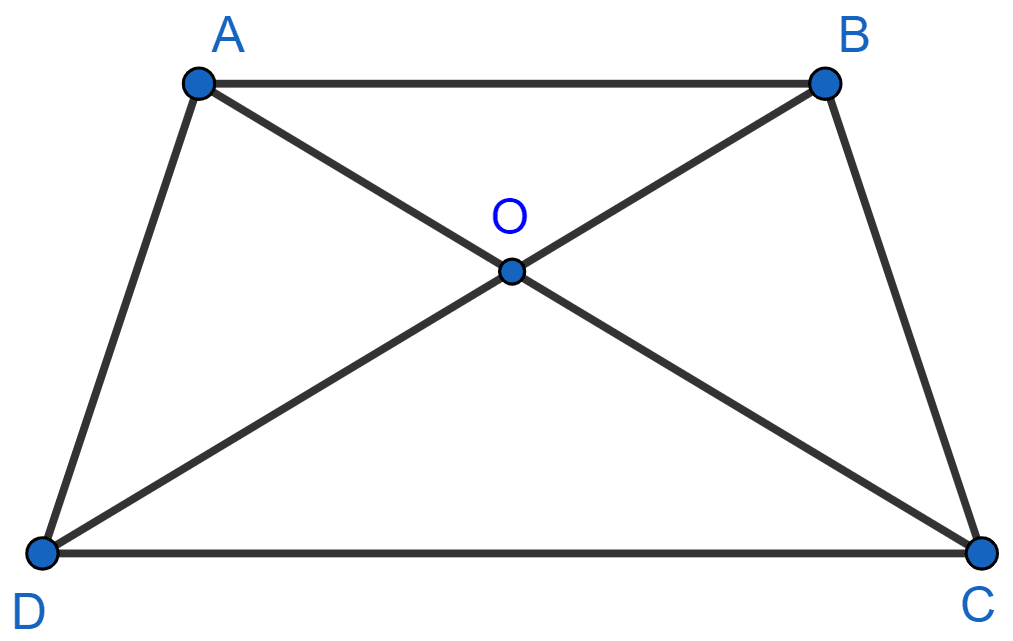
In Δ AOB and Δ COD,

∠AOB = ∠COD (Vertically opposite angles are equal)

∠BAO = ∠DCO (Alternate angles are equal)

⇒ Δ AOB ∼ Δ COD (By A.A. axiom)

We know that,

Ratio of corresponding sides of a similar triangle are proportional.

Hence, proved that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$.

In the given figure, $\dfrac{QR}{QS} = \dfrac{QT}{PR}$ and ∠1 = ∠2. Show that △ PQS ~ △ TQR.

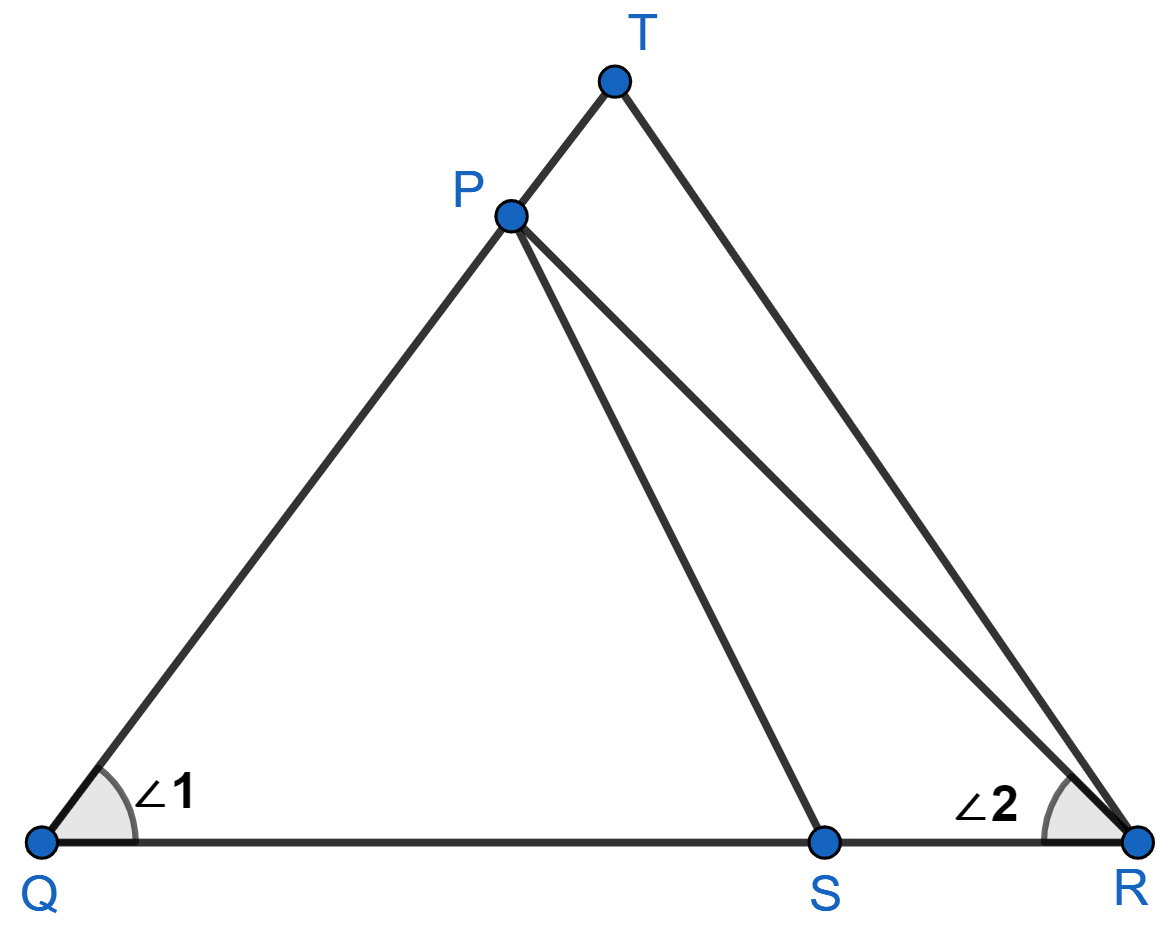
Answer

In Δ PQR,

∠1 = ∠2 (Given)

⇒ PR = PQ (In a triangle sides opposite to equal angles are equal)

In Δ PQS and Δ TQR

⇒ ∠PQS = ∠TQR (Both = ∠1)

Given,

$\Rightarrow \dfrac{QR}{QS} = \dfrac{QT}{PR}$

Since, PR = PQ.

$\therefore \dfrac{QR}{QS} = \dfrac{QT}{PQ}$

∴ Δ PQS ~ Δ TQR (By SAS criterion)

Hence, proved that △ PQS ~ △ TQR.

S and T are points on sides PR and QR of △ PQR such that ∠P = ∠RTS. Show that △ RPQ ~ △ RTS.

Answer

In Δ RPQ and Δ RTS,

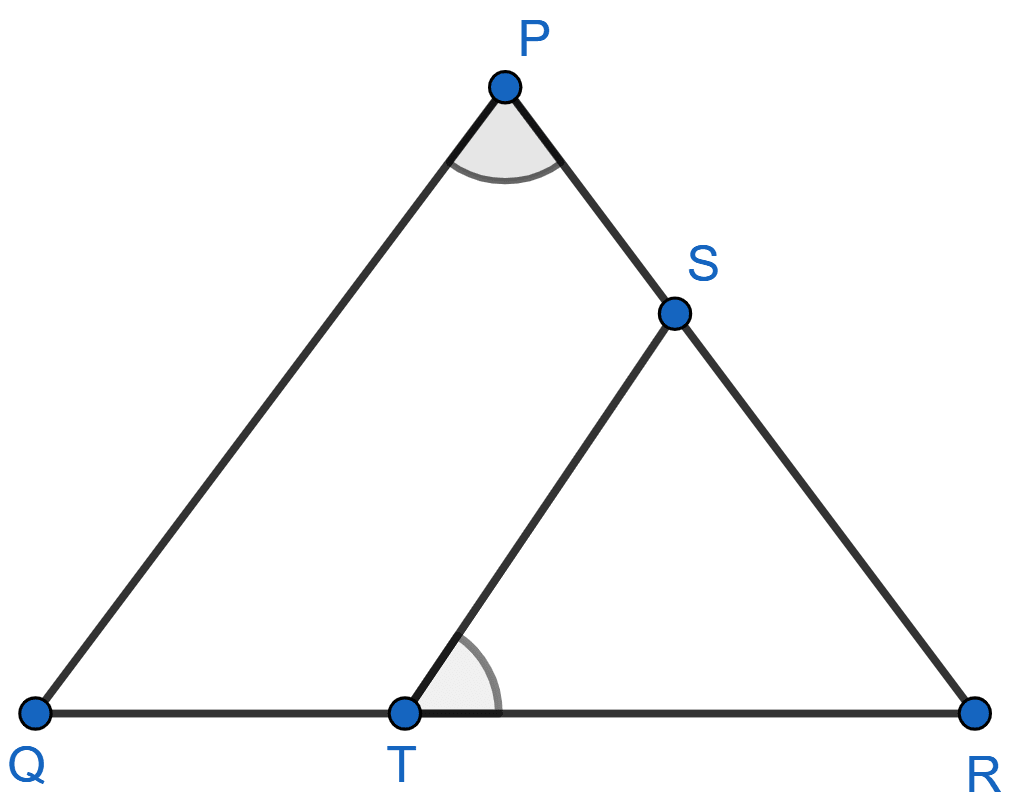
⇒ ∠RPQ = ∠RTS (Given)

⇒ ∠PRQ = ∠TRS (Common angle)

∴ Δ RPQ ∼ Δ RTS (By A.A. axiom)

Hence, proved that △ RPQ ~ △ RTS.

In given figure, if △ ABE ≅ Δ ACD, show that
△ ADE ∼ Δ ABC.

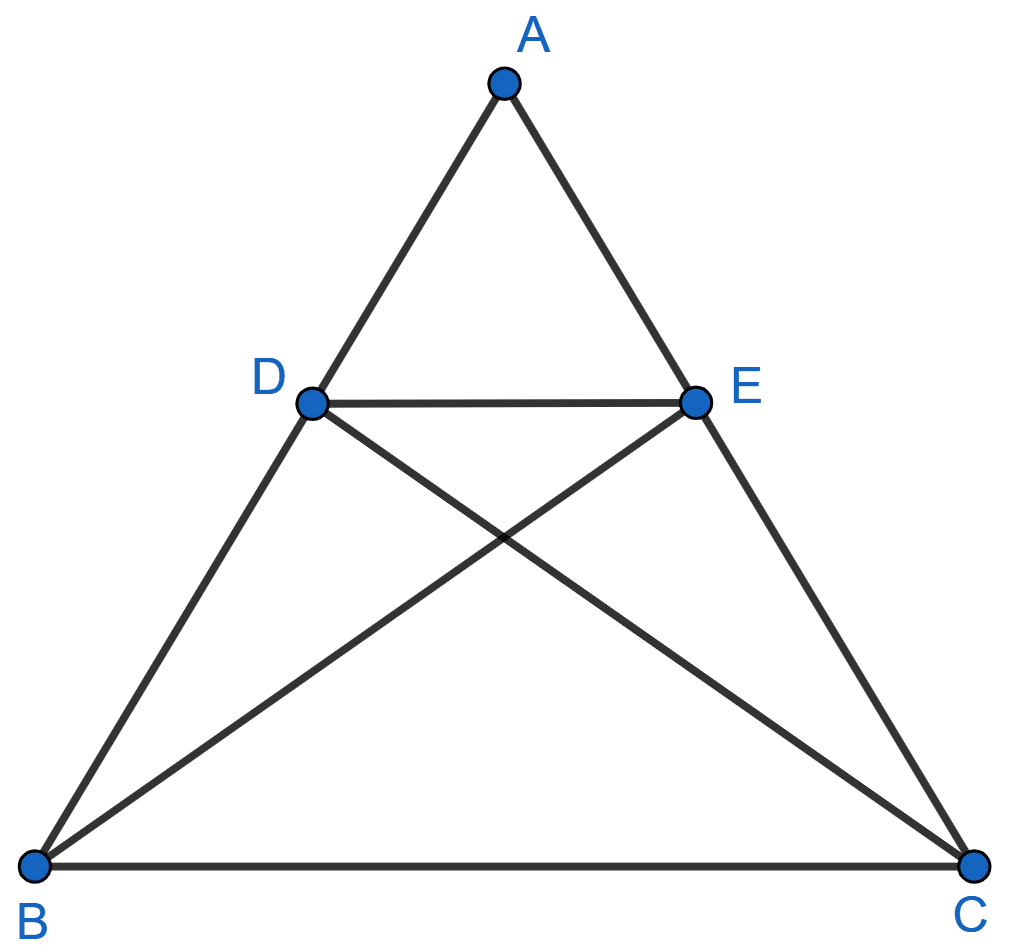
Answer

Given,

△ ABE ≅ Δ ACD

We know that,

Corresponding parts of congruent triangle are equal.

⇒ AD = AE = x (let)

⇒ AC = AB = y (let)

In ∆ ADE and ∆ ABC

$\Rightarrow \dfrac{AD}{AB} = \dfrac{AE}{AC} = \dfrac{x}{y}$

⇒ ∠DAE = ∠BAC (Common angle)

∴ ∆ADE ~ ∆ABC (By S.A.S. axiom)

Hence, proved that ∆ADE ~ ∆ABC.

In the given figure, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that:

(i) ∆ AEP ~ ∆ CDP

(ii) ∆ ABD ~ ∆ CBE

(iii) ∆ AEP ~ ∆ ADB

(iv) ∆ PDC ~ ∆ BEC

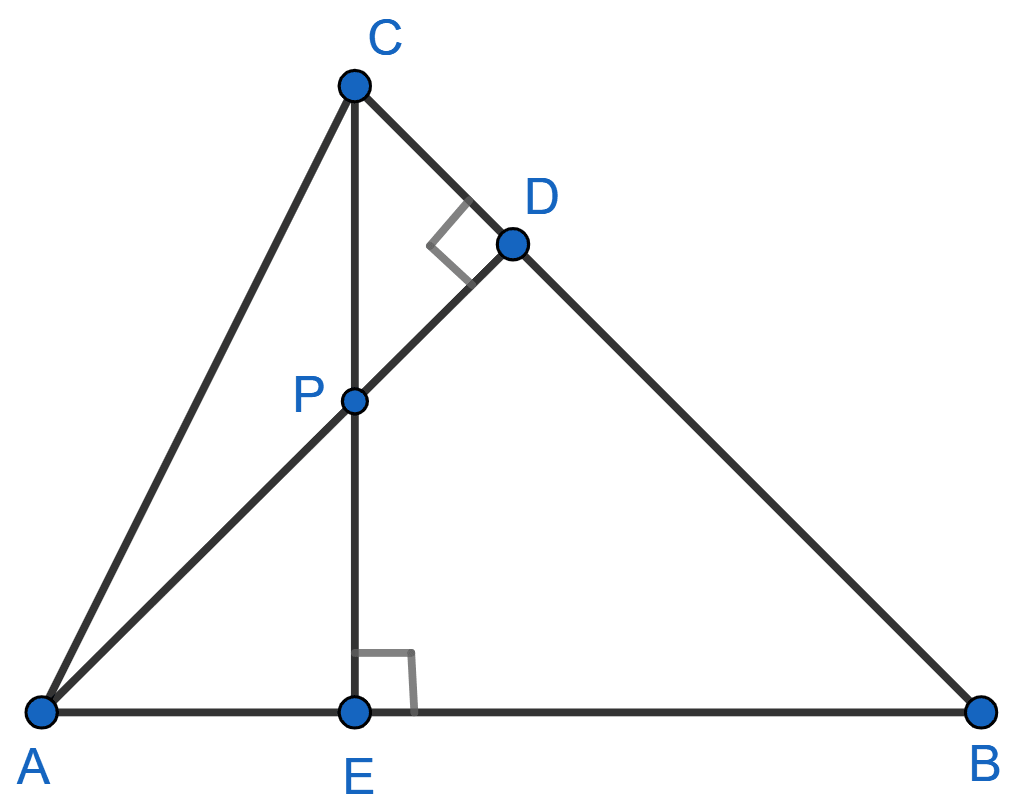
Answer

(i) In Δ AEP and Δ CDP,

⇒ ∠AEP = ∠CDP (Both = 90°)

⇒ ∠APE = ∠CPD (Vertically opposite angles are equal)

⇒ Δ AEP ~ Δ CDP (By A.A. axiom)

Hence, proved that Δ AEP ~ Δ CDP.

(ii) In Δ ABD and Δ CBE,

⇒ ∠ADB = ∠CEB (Both = 90°)

⇒ ∠ABD = ∠CBE (Common angle)

⇒ Δ ABD ~ Δ CBE (By A.A. axiom)

Hence, proved that Δ ABD ~ Δ CBE.

(iii) In Δ AEP and Δ ADB,

⇒ ∠AEP = ∠ADB (Both = 90°)

⇒ ∠PAE = ∠BAD (Common angle)

⇒ Δ AEP ~ Δ ADB (By A.A. axiom)

Hence, proved that Δ AEP ~ Δ ADB.

(iv) In Δ PDC and Δ BEC,

⇒ ∠PDC = ∠BEC (Both = 90°)

⇒ ∠PCD = ∠BCE (Common angle)

⇒ Δ PDC ~ Δ BEC (By A.A. axiom)

Hence, proved that Δ PDC ~ Δ BEC.

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that △ ABE ~ △ CFB.

Answer

Parallelogram ABCD is shown in the figure below:

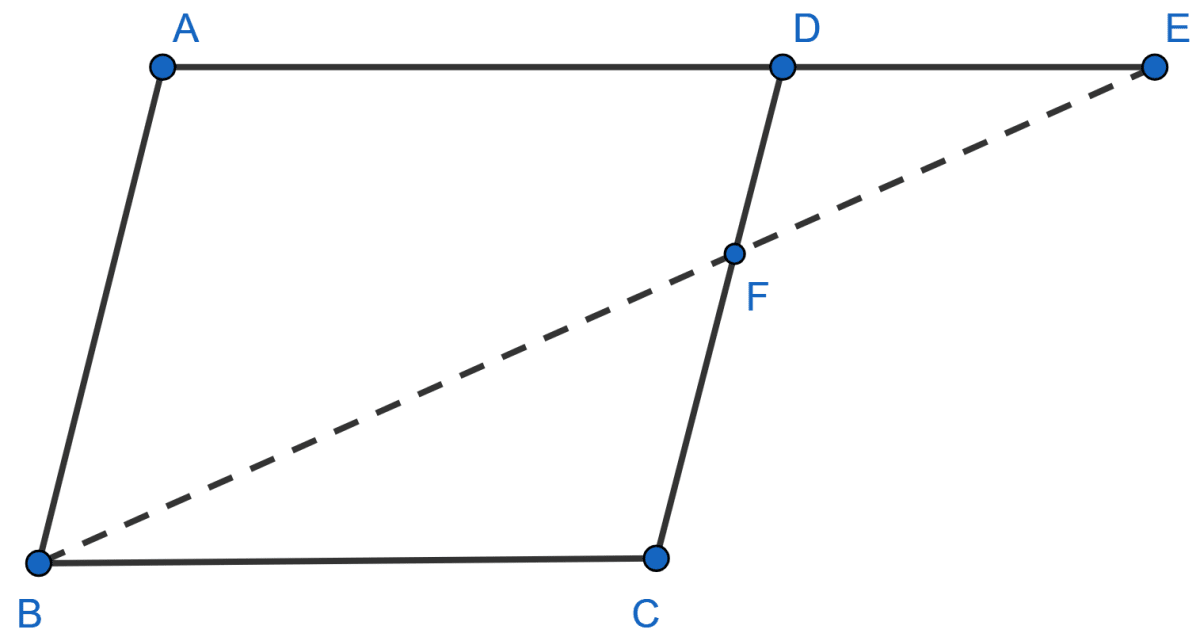
In Δ ABE and Δ CFB,

⇒ ∠BAE = ∠FCB (Opposite angles of a parallelogram are equal)

⇒ ∠AEB = ∠FBC [AE || BC and EB is a transversal, alternate interior angles]

∴ Δ ABE ~ Δ CFB (By A.A. axiom)

Hence, proved that △ ABE ~ △ CFB.

In the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :

(i) Δ ABC ~ Δ AMP

(ii) $\dfrac{CA}{PA} = \dfrac{BC}{MP}$

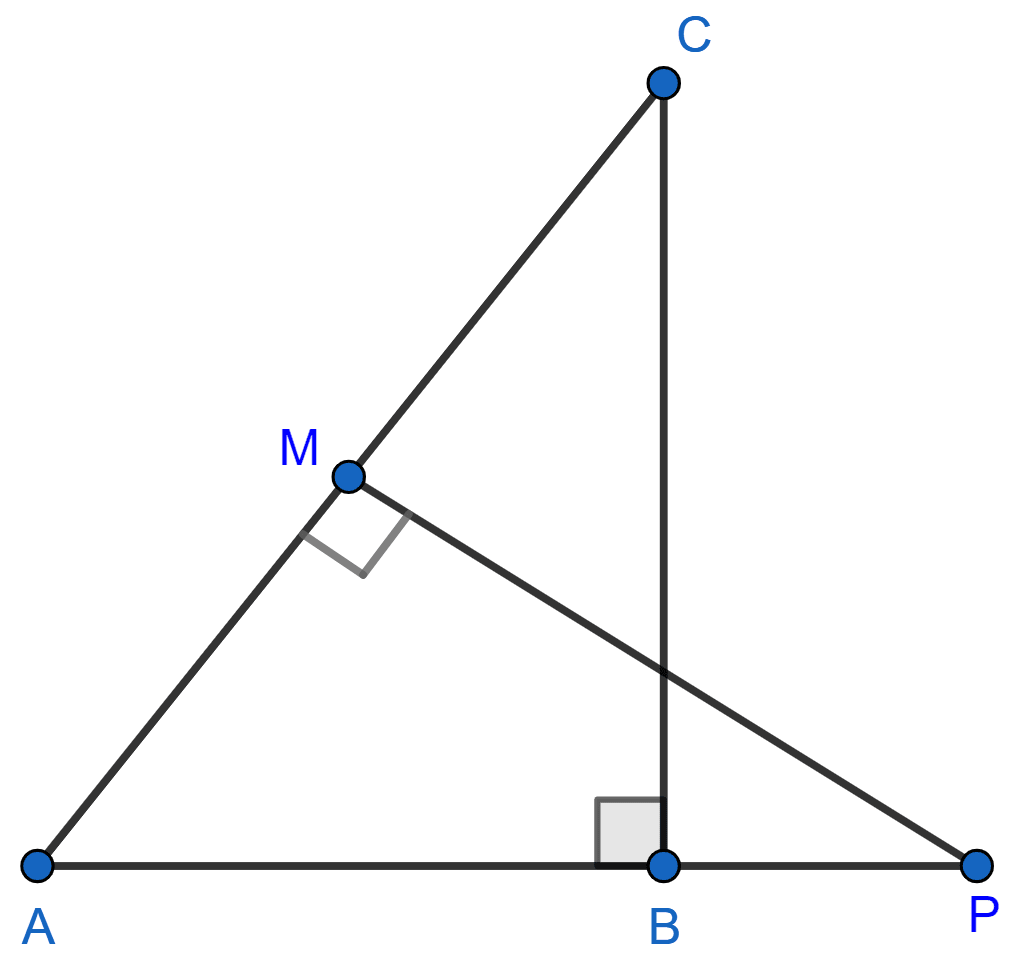
Answer

(i) In Δ ABC and Δ AMP,

⇒ ∠ABC = ∠AMP (Both = 90°)

⇒ ∠BAC = ∠MAP (Common angle)

∴ Δ ABC ∼ Δ AMP (By A.A. axiom)

Hence, proved that Δ ABC ~ Δ AMP.

(ii) We know that,

Ratio of corresponding sides in two similar triangles are proportional.

In Δ ABC and Δ AMP,

$\dfrac{CA}{PA} = \dfrac{BC}{MP}$

Hence, proved that $\dfrac{CA}{PA} = \dfrac{BC}{MP}$.

CD and GH are respectively the bisectors of Δ ACB and Δ EGF such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:

(i) $\dfrac{CD}{GH} = \dfrac{AC}{FG}$

(ii) Δ DCB ~ Δ HGE

(iii) Δ DCA ~ Δ HGF

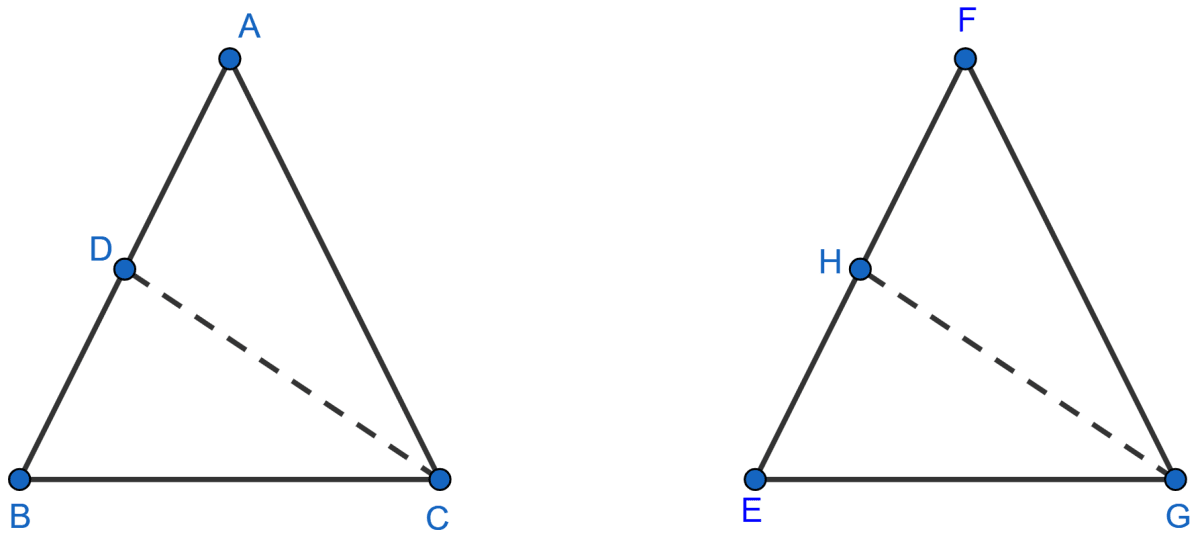
Answer

(i) Given,

∆ ABC ~ ∆ FEG

We know that,

If two triangles are similar, then their corresponding angles are congruent.

⇒ ∠ACB = ∠FGE

⇒ $\dfrac{∠ACB}{2} = \dfrac{∠FGE}{2}$

⇒ ∠ACD = ∠FGH (CD and GH are bisectors of ∠C and ∠G respectively) ..............(1)

In ∆ ADC and ∆ FHG,

⇒ ∠DAC = ∠HFG [∵ ∆ABC ~ ∆FEG]

⇒ ∠ACD = ∠FGH [From equation (1)]

∴ ∆ ADC ~ ∆ FHG (By A.A. axiom)

We know that,

Ratio of corresponding sides in similar triangle are proportional.

∴ $\dfrac{CD}{GH} = \dfrac{AC}{FG}$.

Hence, proved that $\dfrac{CD}{GH} = \dfrac{AC}{FG}$.

(ii) In ∆ DCB and ∆ HGE,

⇒ ∠DBC = ∠HEG [∵ ∆ ABC ~ ∆ FEG]

⇒ ∠DCB = ∠HGE [∵ $\dfrac{∠ACB}{2} = \dfrac{∠FGE}{2}$]

∴ ∆ DCB ~ ∆ HGE (By A.A. axiom)

Hence, proved that ∆ DCB ~ ∆ HGE.

(iii) In ∆ DCA and ∆ HGF,

⇒ ∠DAC = ∠HFG [∆ ABC ~ ∆ FEG]

⇒ ∠ACD = ∠FGH [From (1)]

∴ ∆ DCA ~ ∆ HGF (By A.A. axiom)

Hence, proved that ∆ DCA ~ ∆ HGF.

In the figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that △ ABD ~ △ ECF.

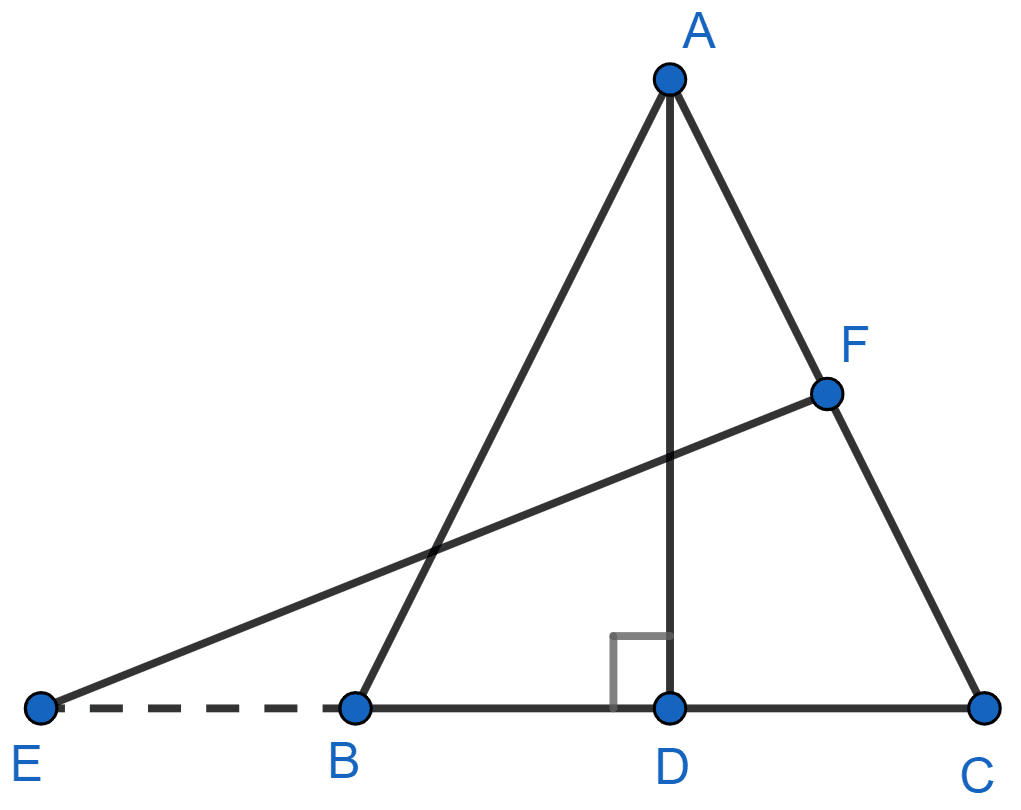
Answer

In Δ ABC,

AB = AC (Given)

∠ABC = ∠ACB (As angles opposite to equal sides are equal.) ......(1)

From figure,

∠ABD = ∠ABC and ∠ACB = ∠ECF

Substituting values of ∠ABC and ∠ACB in equation (1), we get :

⇒ ∠ABD = ∠ECF

In Δ ABD and Δ ECF,

⇒ ∠ADB = ∠EFC = 90° [∵ AD ⊥ BC and EF ⊥ AC]

⇒ ∠ABD = ∠ECF [Proved above]

∴ Δ ABD ~ Δ ECF (By A.A. axiom)

Hence, proved that Δ ABD ~ Δ ECF.

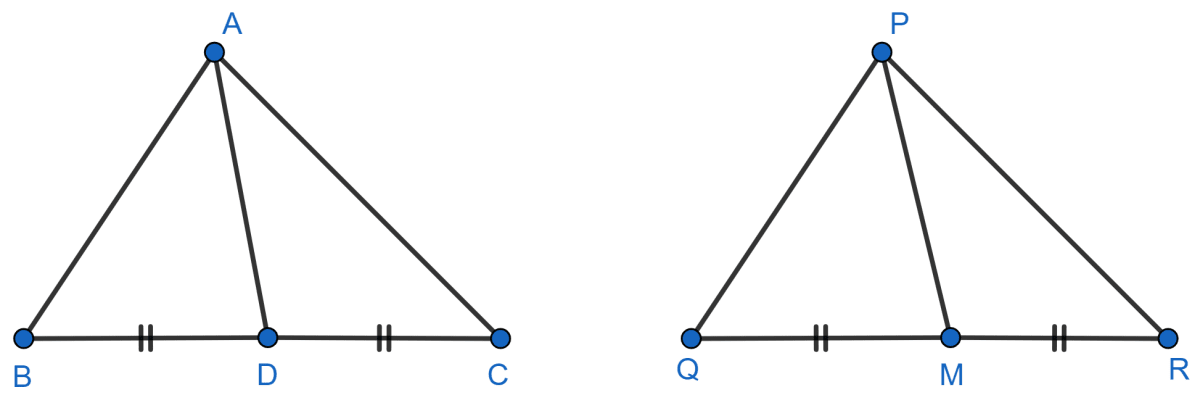
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of △ PQR. Show that △ ABC ~ △ PQR.

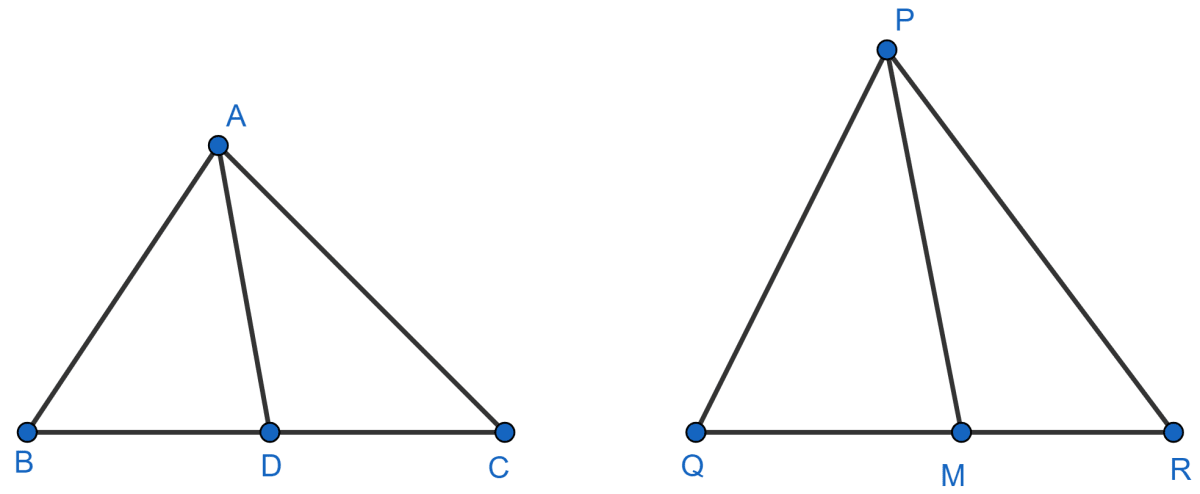
Answer

In Δ ABC and Δ PQR,

As, sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of △ PQR.

$\dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{AD}{PM}$ .......(1)

AD and PM are median of Δ ABC and Δ PQR respectively.

$\therefore \dfrac{BD}{QM} = \dfrac{\dfrac{BC}{2}}{\dfrac{QR}{2}} = \dfrac{BC}{QR}.$

Substituting value of $\dfrac{BC}{QR}$ from above equation in (1), we get :

⇒ $\dfrac{AB}{PQ} = \dfrac{BD}{QM} = \dfrac{AD}{PM}$

∴ Δ ABD ∼ Δ PQM [By SSS axiom]

In Δ ABC and Δ PQR,

⇒ $\dfrac{AB}{PQ} = \dfrac{BC}{QR}$ [Given]

⇒ ∠ABC = ∠PQR [∵ Δ ABD ∼ Δ PQM]

∴ Δ ABC ∼ Δ PQR [By S.A.S. axiom]

Hence, proved that Δ ABC ∼ Δ PQR.

D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA² = CB.CD.

Answer

Δ ABC is shown in the figure below:

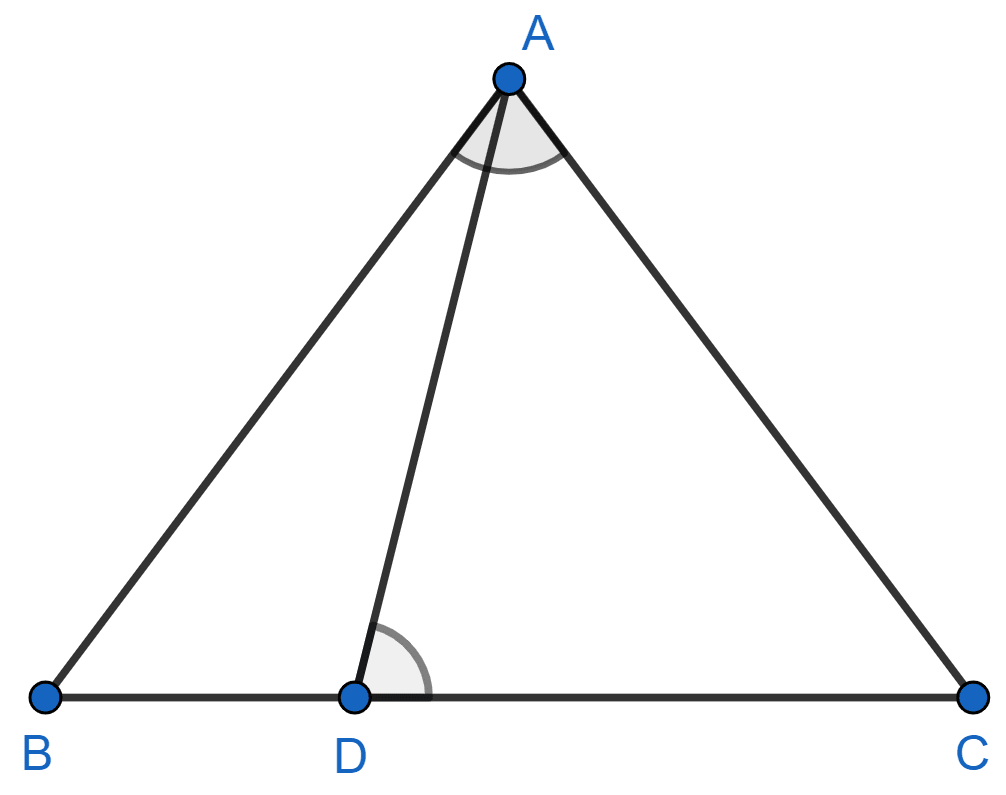
In Δ ABC and Δ DAC,

⇒ ∠BAC = ∠ADC (Given)

⇒ ∠ACB = ∠ACD (Common angles)

∴ Δ ABC ∼ Δ DAC (By A.A. axiom)

We know that,

Corresponding sides of similar triangle are proportional.

$\therefore \dfrac{CA}{CD} = \dfrac{CB}{CA}$

⇒ CA² = CB × CD.

Hence, proved that CA² = CB × CD.

Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that Δ ABC ~ Δ PQR.

Answer

Δ ABC and Δ PQR are shown in the figure below:

Produce AD to E so that AD = DE. Join CE

Similarly, produce PM to N such that PM = MN , and join RN.

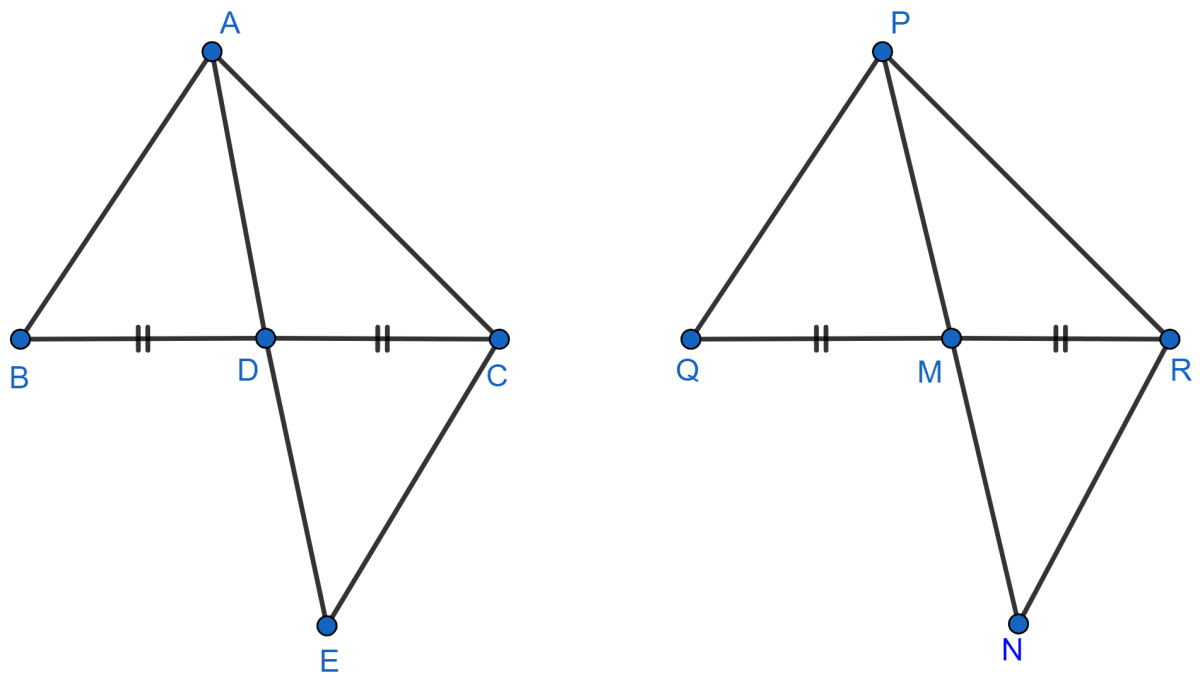
In Δ ABD and Δ CDE,

⇒ AD = DE [By Construction]

⇒ BD = DC [AD is the median]

⇒ ∠ADB = ∠CDE [Vertically opposite angles are equzl]

∴ Δ ABD ≅ Δ ECD [By S.A.S. axiom]

⇒ AB = CE [C.P.C.T.] ...........(1)

Also, in Δ PQM and Δ MNR,

⇒ PM = MN [By Construction]

⇒ QM = MR [PM is the median]

⇒ ∠PMQ = ∠NMR [Vertically opposite angles are equal]

∴ Δ PQM ≅ Δ NRM [By SAS axiom]

⇒ PQ = RN [C.P.C.T.]............(2)

Now,

$\dfrac{AB}{PQ} = \dfrac{AC}{PR} = \dfrac{AD}{PM}$ [Given]

⇒ $\dfrac{CE}{RN} = \dfrac{AC}{PR} = \dfrac{AD}{PM}$ [from (1) and (2)]

⇒ $\dfrac{CE}{RN} = \dfrac{AC}{PR} = \dfrac{2AD}{2PM}$

⇒ $\dfrac{CE}{RN} = \dfrac{AC}{PR} = \dfrac{AE}{PN}$ [ 2AD = AE and 2PM = PN ]

∴ Δ ACE ~ Δ PRN [By SSS similarity criterion]

∴ ∠CAE = ∠RPN

Similarly, ∠BAE = ∠QPN

Hence, ∠CAE + ∠BAE = ∠RPN + ∠QPN

⇒ ∠BAC = ∠QPR

⇒ ∠A = ∠P ....(2)

Now, In Δ ABC and Δ PQR,

$\dfrac{AB}{PQ} = \dfrac{AC}{PR}$

∠A = ∠P [from (2)]

∴ Δ ABC ~ Δ PQR [By SAS similarity criterion]

Hence, Δ ABC ~ Δ PQR.

A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Answer

Let AB be the pole of length 6 m and BC = 4 m is the shadow of pole AB.

Let PQ be the tower and QR = 28 m is the shadow of the tower PQ.

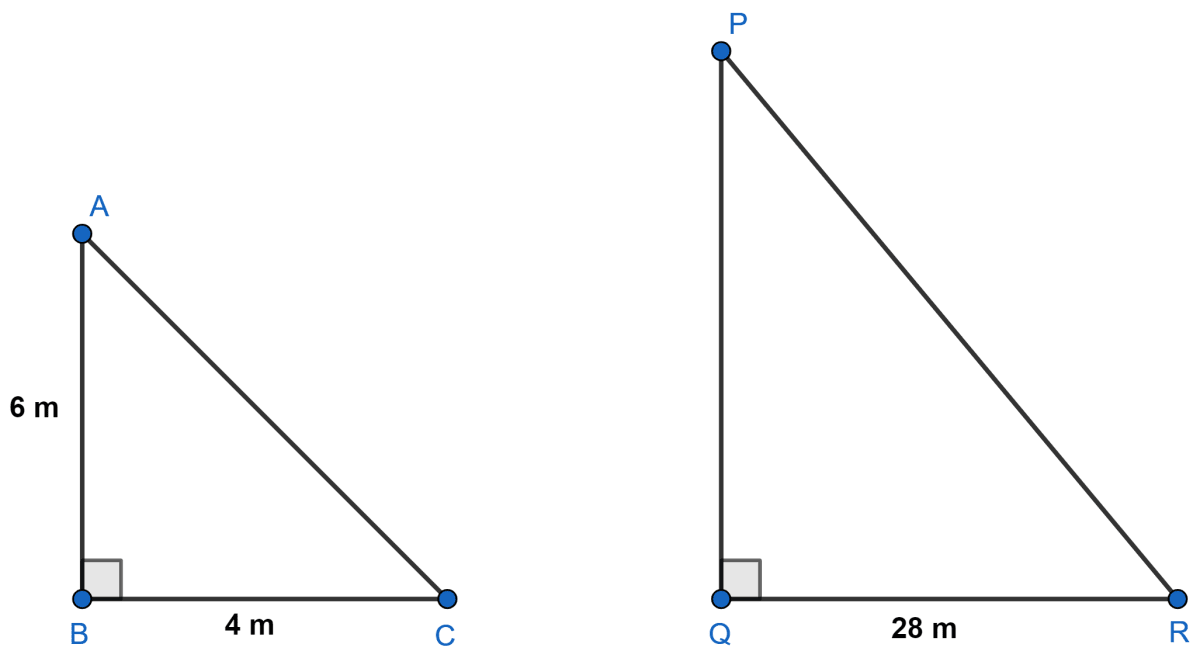
In Δ ABC and Δ PQR,

⇒ ∠ABC = ∠PQR (Both equal to 90°.)

⇒ ∠BAC = ∠QPR (Sunray falls on the pole and tower at the same angle, at the same time)

⇒ Δ ABC ∼ Δ PQR (By A.A. axiom)

We know that,

If two triangles are similar then their corresponding sides are proportional.

$\Rightarrow \dfrac{AB}{PQ} = \dfrac{BC}{QR} \\[1em] \Rightarrow PQ = \dfrac{AB \times QR}{BC} \\[1em] \Rightarrow PQ = \dfrac{6 \times 28}{4} \\[1em] \Rightarrow PQ = 42 \text{ m}.$

Hence, the height of the tower is 42 m.

If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$.

Answer

Given, Δ ABC ∼ Δ PQR

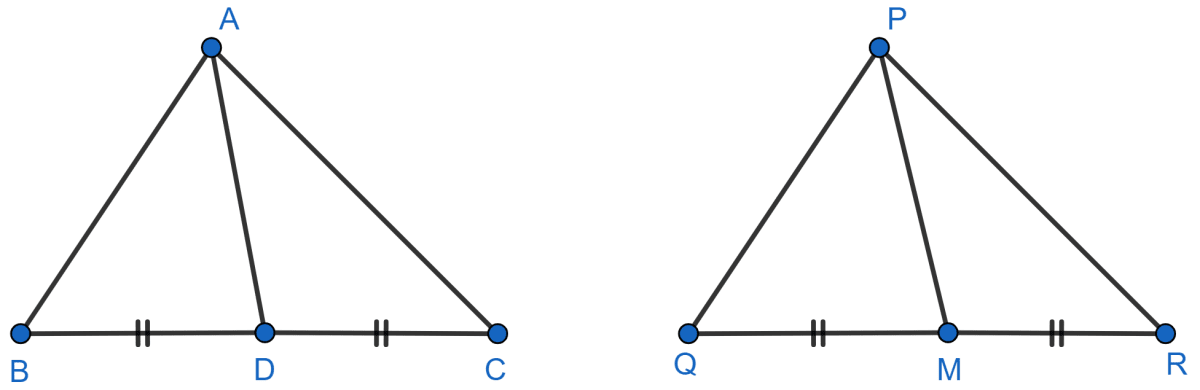
⇒ ∠ABC = ∠PQR (corresponding angles in similar triangle are equal)...........(1)

⇒ $\dfrac{AB}{PQ} = \dfrac{BC}{QR}$ (Ratio of corresponding sides of similar triangle are proportional)

⇒ $\dfrac{AB}{PQ} = \dfrac{\dfrac{BC}{2}}{\dfrac{QR}{2}}$

⇒ $\dfrac{AB}{PQ} = \dfrac{BD}{QM}$ (As D and M are mid-points of BC and QR) .........(2)

In Δ ABD and Δ PQM,

⇒ ∠ABD = ∠PQM [From (1)]

⇒ $\dfrac{AB}{PQ} = \dfrac{BD}{QM}$ [From (2)]

∴ Δ ABD ∼ Δ PQM (By S.A.S. axiom)

We know that,

Ratio of corresponding sides of similar triangle are similar.

$\therefore \dfrac{AB}{PQ} = \dfrac{BD}{QM} = \dfrac{AD}{PM}$.

Hence, proved that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$..