Surface Areas and Volumes

2 cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.

Answer

By formula,

⇒ Volume of cube = (side)³

⇒ 64 cm³ = (side)³

⇒ (side)³ = 4³

⇒ side = 4 cm.

From figure,

On joining two cubes, length of cuboid = 8 cm, height = 4 cm and breadth = 4 cm.

By formula,

Surface area of cuboid = 2(lb + bh + lh)

Substituting values we get :

Surface area of cuboid = 2(8 × 4 + 4 × 4 + 8 × 4)

= 2(32 + 16 + 32)

= 2 × 80

= 160 cm².

Hence, surface area of cuboid = 160 cm².

A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.

Answer

Given,

Diameter of hemisphere = 14 cm

Radius of hemisphere (r) = $\dfrac{\text{Diameter}}{2} = \dfrac{14}{2}$ = 7 cm.

From figure,

Height of cylindrical vessel (h) = 13 - 7 = 6 cm.

Radius of cylindrical vessel (R) = Radius of hemisphere (r) = 7 cm.

Inner surface area of vessel = Curved surface area of hemisphere + Curved surface area of cylinder

= 2πr² + 2πRh

= 2π(r² + Rh)

= $2 \times \dfrac{22}{7}(7^2 + 7 \times 6)$

= $\dfrac{44}{7} \times (49 + 42)$

= $\dfrac{44}{7} \times 91$

= 44 × 13

= 572 cm².

Hence, inner surface area of vessel = 572 cm².

A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

Answer

From figure,

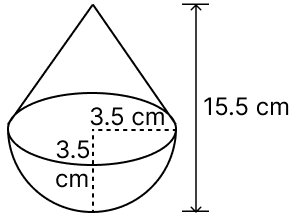
Height of cone (h) = 15.5 - 3.5 = 12 cm.

Radius of cone = Radius of hemisphere = r = 3.5 cm.

By formula,

Slant height (l) = $\sqrt{r^2 + h^2}$

Substituting values we get :

$l = \sqrt{(3.5)^2 + 12^2} \\[1em] = \sqrt{12.25 + 144} \\[1em] = \sqrt{156.25} \\[1em] = 12.5 \text{ cm}.$

Total surface area of toy = Curved surface area of cone + Curved surface area of hemisphere

= πrl + 2πr²

= πr(l + 2r)

= 3.5π(12.5 + 2 × 3.5)

= 3.5π(12.5 + 7)

= $3.5 \times \dfrac{22}{7} \times 19.5$

= 214.5 cm².

Hence, total surface area of toy = 214.5 cm².

A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Answer

The greatest diameter that hemisphere can have is equal to the length of cube i.e., 7 cm.

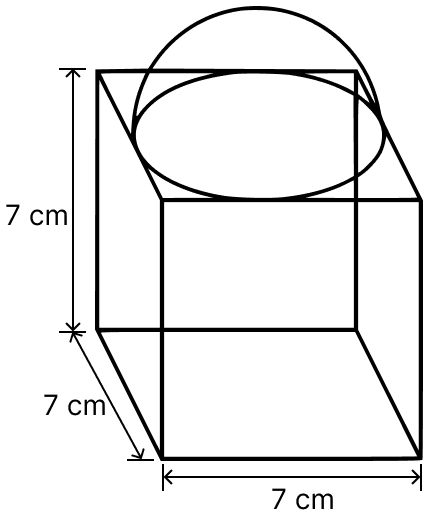
Radius of hemisphere (r) = $\dfrac{7}{2}$ = 3.5 cm

Surface area of solid = Surface area of cubical part - Base area of hemisphere + Curved surface area of hemisphere

= 6(side)² - πr² + 2πr²

= 6 × 7² + πr²

= 6 × 49 + $\dfrac{22}{7} \times (3.5)^2$

= 294 + 38.5 = 332.5 cm².

Hence, greatest diameter = 7 cm and surface area of solid = 332.5 cm².

A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

Answer

Given,

Diameter of hemispherical depression = $l$ units.

Radius of hemispherical vessel = $\dfrac{l}{2}$ units.

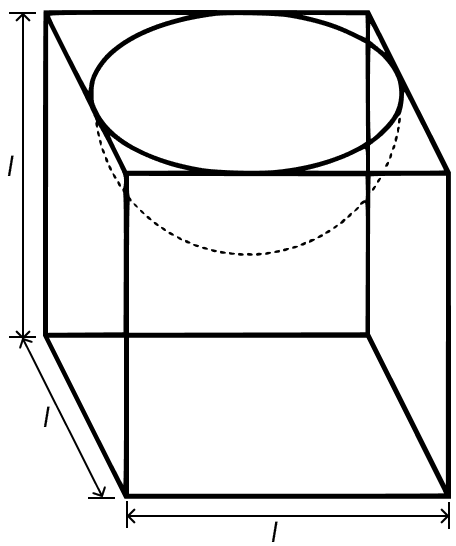
From figure,

Surface area of remaining solid = Surface area of cube + Curved surface area of hemisphere - Area of base of hemisphere

= 6(side)² + 2πr² - πr²

= 6(side)² + πr²

= 6l² + π $\times \Big(\dfrac{l}{2}\Big)^2$

= 6l² + $\dfrac{l^2}{4}π$

= $\dfrac{24l^2 + l^2π}{4}$

= $\dfrac{l^2}{4}(24 + π)$.

Hence, surface area of the remaining solid = $\dfrac{l^2}{4}(24 + π)$.

A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

Answer

From figure,

Diameter of capsule (d) = 5 mm

Radius of capsule (r) = $\dfrac{d}{2} = \dfrac{5}{2}$ = 2.5 mm

From figure

Radius of cylindrical portion = Radius of hemispherical portion = Radius of capsule (r) = 2.5 mm.

Height of cylindrical portion (h) = 14 - (2.5 + 2.5) = 14 - 5 = 9 mm.

Surface area of capsule = Curved surface area of cylindrical portion + 2 × Curved surface area of hemispherical portion

= 2πrh + 2 × 2πr²

= 2πrh + 4πr²

= 2πr(h + 2r)

= $2 \times \dfrac{22}{7} \times 2.5 \times (9 + 2 \times 2.5)$

= $2 \times \dfrac{22}{7} \times 2.5 \times 14$

= $\dfrac{1540}{7}$ = 220 mm².

Hence, surface area of capsule = 220 mm².

A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹ 500 per m². (Note that the base of the tent will not be covered with canvas.)

Answer

Given,

Diameter of cylindrical part (d) = 4 m

Radius of cylindrical part = $\dfrac{d}{2} = \dfrac{4}{2}$ = 2 m,

Height of cylindrical part (h) = 2.1 m

Slant height of conical part (l) = 2.8 m

From figure,

Radius of conical part = Radius of cylindrical part = r = 2 m.

Area of canvas for making tent = Curved surface area of conical part + Curved surface area of cylindrical portion

= πrl + 2πrh

= πr(l + 2h)

= $\dfrac{22}{7} \times 2 \times (2.8 + 2 \times 2.1)$

= $\dfrac{44}{7} \times (2.8 + 4.2)$

= $\dfrac{44}{7} \times 7$

= 44 m².

Cost of canvas = Area of canvas required × Cost per square units

= 44 × 500

= ₹ 22000.

Hence, area of canvas required for making tent = 44 m² and cost of canvas = ₹ 22000.

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².

Answer

Given,

Diameter of solid cylinder (d) = 1.4 cm

Radius of solid cylinder (r) = $\dfrac{d}{2} = \dfrac{1.4}{2}$ = 0.7 cm.

Height of cylinder (h) = 2.4 cm

Height of conical cavity = Height of cylinder = h = 2.4 cm.

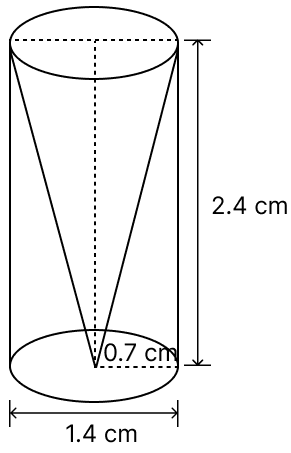
From figure,

Radius of conical cavity = Radius of cylinder = r = 0.7 cm.

By formula,

Slant height of cone (l) = $\sqrt{r^2 + h^2}$

Substituting value we get :

$l = \sqrt{(0.7)^2 + (2.4)^2} \\[1em] = \sqrt{0.49 + 5.76} \\[1em] = \sqrt{6.25} \\[1em] = 2.5 \text{ cm}.$

Total surface area of remaining solid = Curved surface area of cylinder + Curved surface area of cone + Base area of cylindrical portion

Substituting values we get :

Total surface area of remaining solid = 2πrh + πrl + πr²

= πr(2h + l + r)

= $\dfrac{22}{7}$ x 0.7 x (2 x 2.4 + 2.5 + 0.7)

= 22 x 0.1 x (4.8 + 2.5 + 0.7)

= 2.2 x 8

= 17.6 ≈ 18 cm²

Hence, the total surface area of the remaining solid = 18 cm².

A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

Answer

Given,

Height of cylinder = 10 cm

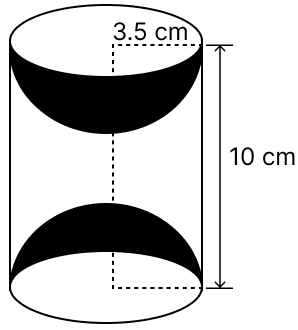
From figure,

Radius of base of cylinder = Radius of hemisphere = r = 3.5 cm

From figure,

Total surface area of article = Curved surface area of cylinder + 2 × Curved surface area of each hemisphere

= 2πrh + 2 × 2πr²

= 2πr(h + 2r)

Substituting values we get :

$= 2 \times \dfrac{22}{7} \times 3.5 \times (10 + 2 \times 3.5) \\[1em] = 2 \times 22 \times 0.5 \times (10 + 7) \\[1em] = 22 \times 1 \times (10 + 7) \\[1em] = 22 \times 17 \\[1em] = 374 \text{ cm}^2.$

Hence, the total surface area of the article is 374 cm².

A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.

Answer

Given,

Radius of cone = Radius of hemisphere = r = 1 cm

Height of cone (h) = 1 cm

Volume of solid = Volume of cone + Volume of hemisphere

$= \dfrac{1}{3}πr^2h + \dfrac{2}{3}πr^3 \\[1em] = \dfrac{πr^2}{3}(h + 2r) \\[1em] = \dfrac{π \times (1)^2}{3} \times (1 + 2 \times 1) \\[1em] = \dfrac{π \times 1}{3} \times (1 + 2) \\[1em] = \dfrac{π}{3} \times 3 \\[1em] = π \text{ cm}^3.$

Hence, volume of solid = π cm³.

Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)

Answer

Given,

Height of each cone (h) = 2 cm

Diameter of model (d) = 3 cm

From figure,

Radius of each cone = Radius of cylinder = r = $\dfrac{d}{2} = \dfrac{3}{2}$ = 1.5 cm

Height of cylinder (H) = 12 - 2 - 2 = 8 cm.

Volume of air inside model = Volume of cylinder + 2 × Volume of each cone

= πr²H + $2 \times \dfrac{1}{3}πr^2h$

= πr²$\Big(H + \dfrac{2}{3}h\Big)$

$= \dfrac{22}{7} \times (1.5)^2 \times \Big(8 + \dfrac{2}{3} \times 2\Big) \\[1em] = \dfrac{22}{7} \times 2.25 \times \Big(8 + \dfrac{4}{3}\Big) \\[1em] = \dfrac{22}{7} \times 2.25 \times \Big(\dfrac{24 + 4}{3}\Big) \\[1em] = \dfrac{22}{7} \times 2.25 \times \dfrac{28}{3} \\[1em] = \dfrac{1386}{21} \\[1em] = 66 \text{ cm}^3.$

Hence volume of air contained in model = 66 cm³.

A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm.

Answer

From figure,

Diameter of gulab jamun (d) = 2.8 cm

Radius of cylindrical portion = Radius of hemispherical portion = r = $\dfrac{d}{2} = \dfrac{2.8}{2}$ = 1.4 cm.

Length of cylindrical portion (h) = 5 - 1.4 - 1.4 = 2.2 cm

Volume of each gulab jamun = Volume of cylindrical portion + 2 × Volume of each hemispherical portion

$= πr^2h + 2 \times \dfrac{2}{3}πr^3 \\[1em] = πr^2\Big(h + \dfrac{4}{3}r\Big) \\[1em] = \dfrac{22}{7} \times (1.4)^2 \times \Big(2.2 + \dfrac{4}{3} \times 1.4\Big) \\[1em] = 22 \times 0.2 \times 1.4 \times \Big(2.2 + \dfrac{5.6}{3}\Big) \\[1em] = 22 \times 0.2 \times 1.4 \times \dfrac{6.6 + 5.6}{3} \\[1em] = 22 \times 0.2 \times 1.4 \times \dfrac{12.2}{3} \\[1em] = \dfrac{75.152}{3} \\[1em] = 25.05 \text{ cm}^3.$

Volume of 45 gulab jamuns = 45 × 25.05 = 1127.28 cm³.

Given,

A gulab jamun, contains sugar syrup up to about 30% of its volume.

∴ Sugar syrup in 45 gulab jamuns = 30% of volume of 45 gulab jamuns

= $\dfrac{30}{100} \times 1127.28$ = 338.184 ≈ 338 cm³.

Hence, approximately 338 cm³ of sugar syrup would be found in 45 gulab jamuns.

A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.

Answer

Given,

Length of cuboid (l) = 15 cm

Breadth of cuboid (b) = 10 cm

Height of cuboid (h) = 3.5 cm

Radius of each conical depression (r) = 0.5 cm

Depth of each conical depression (H) = 1.4 cm

From figure,

Volume of wood in stand = Volume of cuboid - 4 × Volume of each conical depression

= lbh - 4 × $\dfrac{1}{3}πr^2H$

= 15 × 10 × 3.5 - $4 \times \dfrac{1}{3} \times \dfrac{22}{7} \times 0.5 \times 0.5 \times 1.4$

= 525 - $\dfrac{22}{21} \times 1.4$

= 525 - $\dfrac{4.4}{3}$

= 525 - 1.47 = 523.53 cm³.

Hence, volume of wood in entire stand = 523.53 cm³.

A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Answer

Given,

Radius of cone (R) = 5 cm

Height of cone (H) = 8 cm

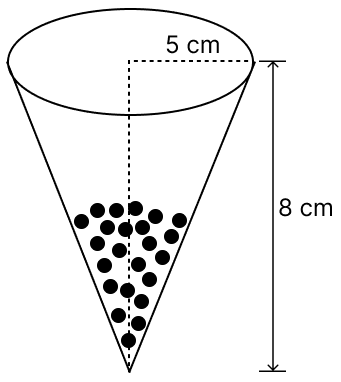
By formula,

Volume of cone = $\dfrac{1}{3}πR^2H$

Substituting values we get :

$= \dfrac{1}{3} \times π \times 5^2 \times 8 \\[1em] = \dfrac{200π}{3} \text{ cm}^3.$

Volume of water in vessel = Volume of cone = $\dfrac{200π}{3}$ cm³.

Let no. of lead shots be n.

Given,

Radius of lead shots (r) = 0.5 cm

Since,

One-fourth of the water flows out after dropping lead shots in vessel.

∴ n × Volume of each lead shot = $\dfrac{1}{4} \times$ Volume of water

$\Rightarrow n \times \dfrac{4}{3}πr^3 = \dfrac{1}{4} \times \dfrac{200π}{3} \\[1em] \Rightarrow n \times \dfrac{4}{3}π \times (0.5)^3 = \dfrac{50π}{3} \\[1em] \Rightarrow n = \dfrac{50π \times 3}{4π \times 3 \times (0.5)^3} \\[1em] \Rightarrow n = \dfrac{50}{4 \times 0.125} \\[1em] \Rightarrow = \dfrac{50}{0.5} = 100.$

Hence, 100 lead shots were dropped in vessel.

A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm³ of iron has approximately 8g mass. (Use π = 3.14)

Answer

The below figure shows the solid iron pole consisting of the two cylinders:

Given,

For bigger cylinder :

Diameter (d) = 24 cm

Radius (R) = $\dfrac{d}{2} = \dfrac{24}{2}$ = 12 cm.

Height (H) = 220 cm

Volume = πR²H

= 3.14 × (12)² × 220

= 3.14 × 144 × 220

= 99475.20 cm³

For smaller cylinder :

Radius (r) = 8 cm

Height (h) = 60 cm

Volume = πr²h

= 3.14 × 8² × 60

= 3.14 × 64 × 60

= 12057.60 cm³.

Volume of pole = Volume of bigger cylinder + Volume of smaller cylinder

= 99475.20 + 12057.60 = 111532.80 cm³

Given,

1 cm³ of iron weighs 8 g.

∴ Mass of pole = Volume of pole × 8 g

= 111532.80 × 8 = 892262.4 g = $\dfrac{892262.4}{1000}$ = 892.26 kg.

Hence, mass of pole = 892.26 kg.

A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.

Answer

Given,

Height of right circular cone (h) = 120 cm

Height of cylinder (H) = 180 cm

From figure,

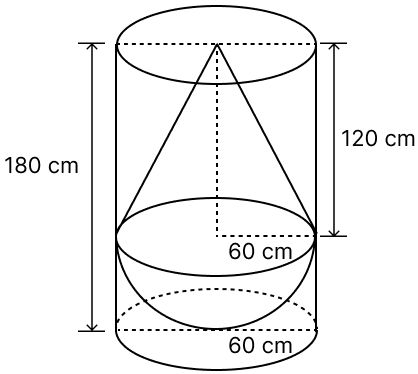
Radius of cylinder = Radius of cone = Radius of hemisphere = r = 60 cm.

Volume of water left in cylinder = Volume of cylinder - Volume of solid

= Volume of cylinder - (Volume of cone + Volume of hemisphere)

$= πr^2H - \Big(\dfrac{1}{3}πr^2h + \dfrac{2}{3}πr^3\Big) \\[1em] = πr^2(H - \dfrac{h}{3} - \dfrac{2}{3}r) \\[1em] = \dfrac{22}{7} \times 60^2 \Big(180 - \dfrac{120}{3} - \dfrac{2}{3} \times 60\Big) \\[1em] = \dfrac{22}{7} \times 3600 \times (180 - 40 - 40) \\[1em] = \dfrac{22}{7} \times 3600 \times 100 \\[1em] = \dfrac{7920000}{7} \\[1em] = 1131428.57143 \text{ cm}^3 \\[1em] = 1131428.57143 \times 10^{-6} \text{ m}^3 \\[1em] = 1.131 \text{ m}^3.$

Hence, volume of water left in cylinder = 1.131 m³.

A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm³. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.

Answer

Given,

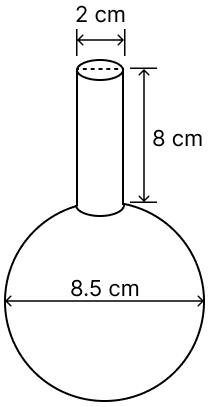
Diameter of sphere (D) = 8.5 cm

Radius of sphere (R) = $\dfrac{D}{2} = \dfrac{8.5}{2}$ = 4.25 cm.

Height of cylindrical neck (h) = 8 cm

Diameter of cylindrical neck (d) = 2 cm

Radius of cylindrical neck (r) = $\dfrac{d}{2} = \dfrac{2}{2}$ = 1 cm.

Volume of glass vessel = Volume of sphere + Volume of cylinder

$= \dfrac{4}{3}πR^3 + πr^2h \\[1em] = π\Big(\dfrac{4}{3}R^3 + r^2h\Big) \\[1em] = 3.14 \times \Big(\dfrac{4}{3} \times (4.25)^3 + 1^2 \times 8\Big) \\[1em] = 3.14 \times \Big(\dfrac{4}{3} \times 76.77 + 1 \times 8\Big) \\[1em] = 3.14 \times \Big(\dfrac{307.0625}{3} + 8\Big) \\[1em] = 3.14 \times (102.35 + 8) \\[1em] = 3.14 \times 110.35 \\[1em] = 346.51 \text{ cm}^3.$

∴ Volume of water in vessel = 346.51 cm^3.

Hence, volume of water in vessel is not equal to 345 cm³.