Mathematics
Vertex A of triangle ABC is (-3, 5) and mid-points of the sides AB and AC are (-4, 4) and (2, -2) respectively. Find :
(i) co-ordinates of vertices B and C.
(ii) equation of line through vertex C and parallel to side AB.
Straight Line Eq
4 Likes
Answer
(i) By mid-point formula,
M =
Let coordinates of B be (a, b) and C be (c, d).
Given,
Mid-point of AB is (-4, 4).
B = (a, b) = (-5, 3).
Given,
Mid-point of AC is (2, -2).
C = (c, d) = (7, -9).
Hence, co-ordinates of B = (-5, 3) and C = (7, -9).
(ii) By formula,
Slope =
Slope of AB = = 1.
We know that,
Slope of parallel lines are equal.
∴ Slope of required line = 1.
By point-slope form,
Equation of line is : y - y1 = m(x - x1)
So, equation of line through vertex C and parallel to side AB is
⇒ y - (-9) = 1(x - 7)
⇒ y + 9 = x - 7
⇒ y = x - 7 - 9
⇒ y = x - 16.
Hence, equation of line through vertex C and parallel to side AB is y = x - 16.
Answered By
2 Likes
Related Questions
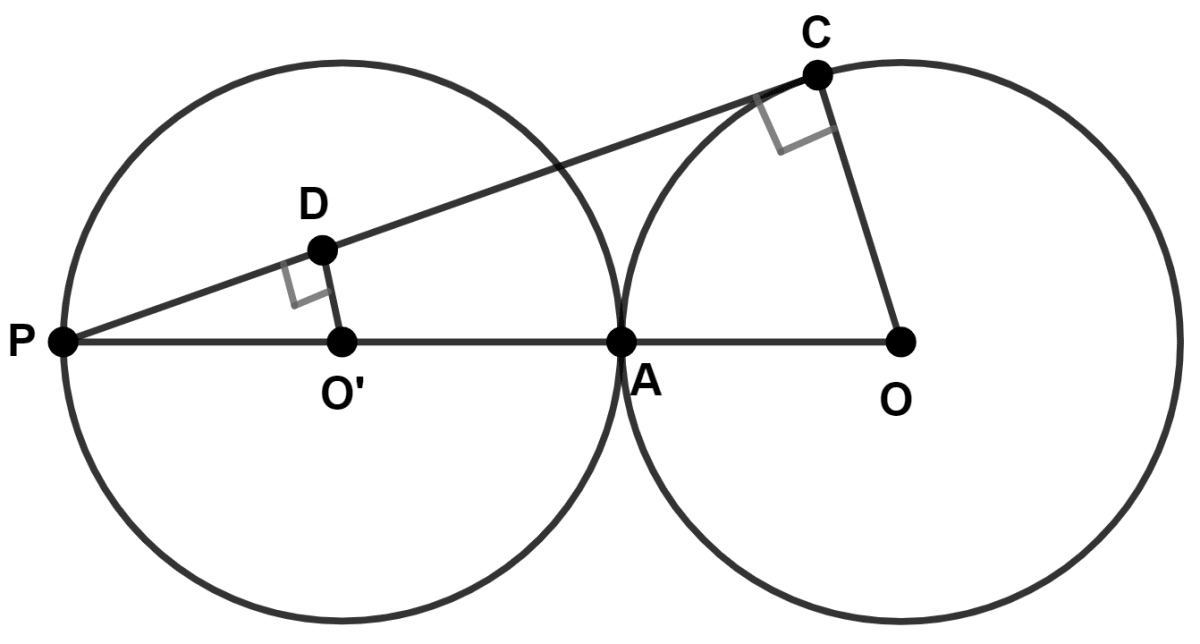
The given figure shows two congruent circles touching each other externally and with centers O' and O as shown. PC is tangent to the circle with center O. Find :
(i)
(ii)
Using remainder theorem factorise 4x3 + 7x2 - 36x - 63 completely.
Prove that :
sin A(1 + tan A) + cos A(1 + cot A) = sec A + cosec A
If the ninth term of an A.P. is zero. Show that its 29th term is twice the 19th term.