Mathematics
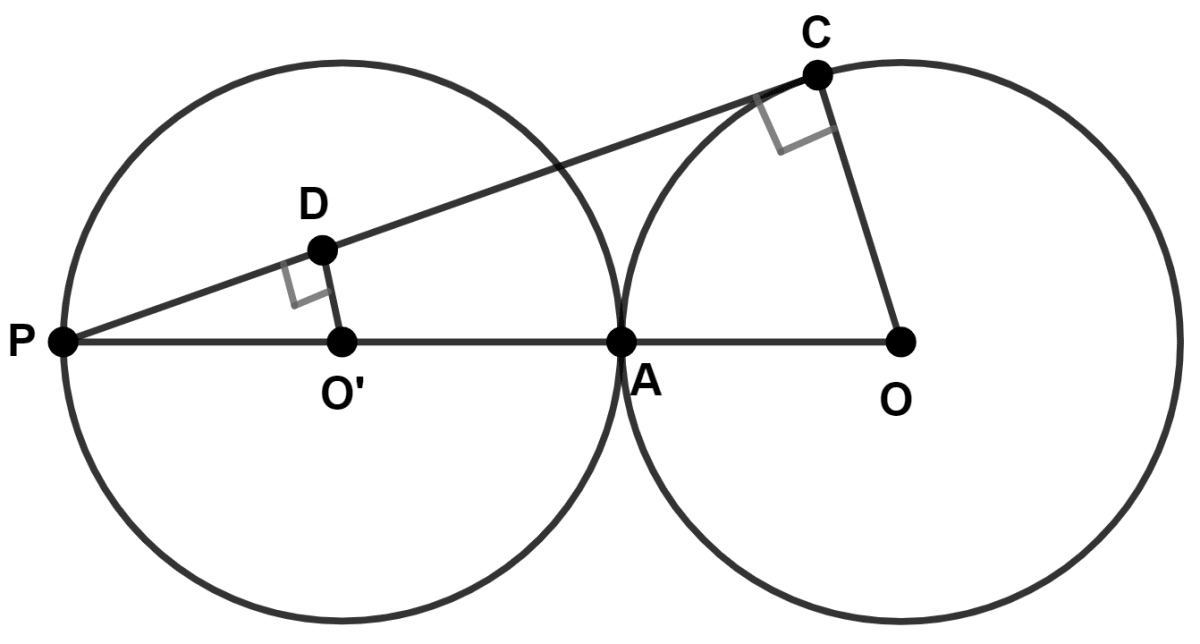
The given figure shows two congruent circles touching each other externally and with centers O' and O as shown. PC is tangent to the circle with center O. Find :
(i)
(ii)
Circles
5 Likes
Answer
(i) Given, circles are congruent, so radius of both circles with be equal.
Let radius of both circles be r.
∴ PO' = AO = r
From figure,
PO = PO' + O'A + AO = r + r + r = 3r.
.
Hence, .
(ii) In △PDO' and △PCO,
∠PDO = ∠PCO = 90°
∠DPO' = ∠CPO (Common)
∴ △PDO' ~ △PCO (By A.A. axiom)
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, .
Answered By
2 Likes
Related Questions
On a graph paper, draw histogram (taking suitable scales) for the following data and then using histogram drawn, find the mode :
Monthly wages No. of workers 1850-1900 32 1900-1950 64 1950-2000 84 2000-2050 100 2050-2100 70 If matrix M = , find M2 - 4M - 4I.
Using remainder theorem factorise 4x3 + 7x2 - 36x - 63 completely.
Vertex A of triangle ABC is (-3, 5) and mid-points of the sides AB and AC are (-4, 4) and (2, -2) respectively. Find :
(i) co-ordinates of vertices B and C.
(ii) equation of line through vertex C and parallel to side AB.