Mathematics
Using ruler and compasses only, construct a parallelogram ABCD with AB = 5 cm, AD = 2.5 cm and ∠BAD = 45°. If the bisector of ∠BAD meets DC at E, prove that ∠AEB is a right angle.
Answer
Steps of construction:
- Draw AB = 5.0 cm.
- At A, construct ∠BAP = 45°.
- With A as centre and radius 2.5 cm cut the line AP at D.
- With D as centre and radius 5.0 cm, draw an arc.
- With B as center and radius 2.5 cm, draw an arc to meet the previous arc at C.
- Join BC and CD. Then, ABCD is the required parallelogram
Draw the bisector of ∠BAD, which cuts DC at E and join EB.
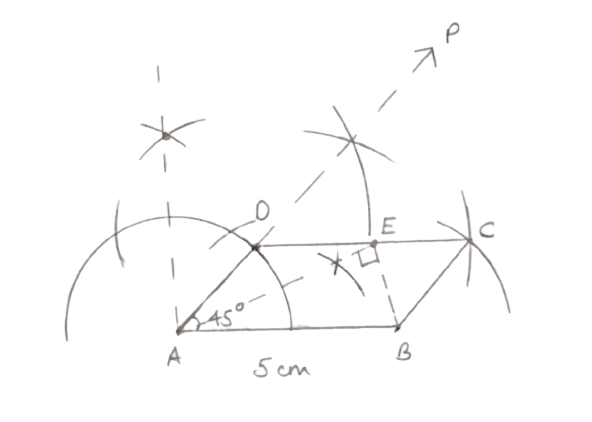
On measuring ∠AEB, it is equal to 90°.
Hence, proved that ∠AEB is a right angle.
Related Questions
Find the size of each lettered angle in the following figure:

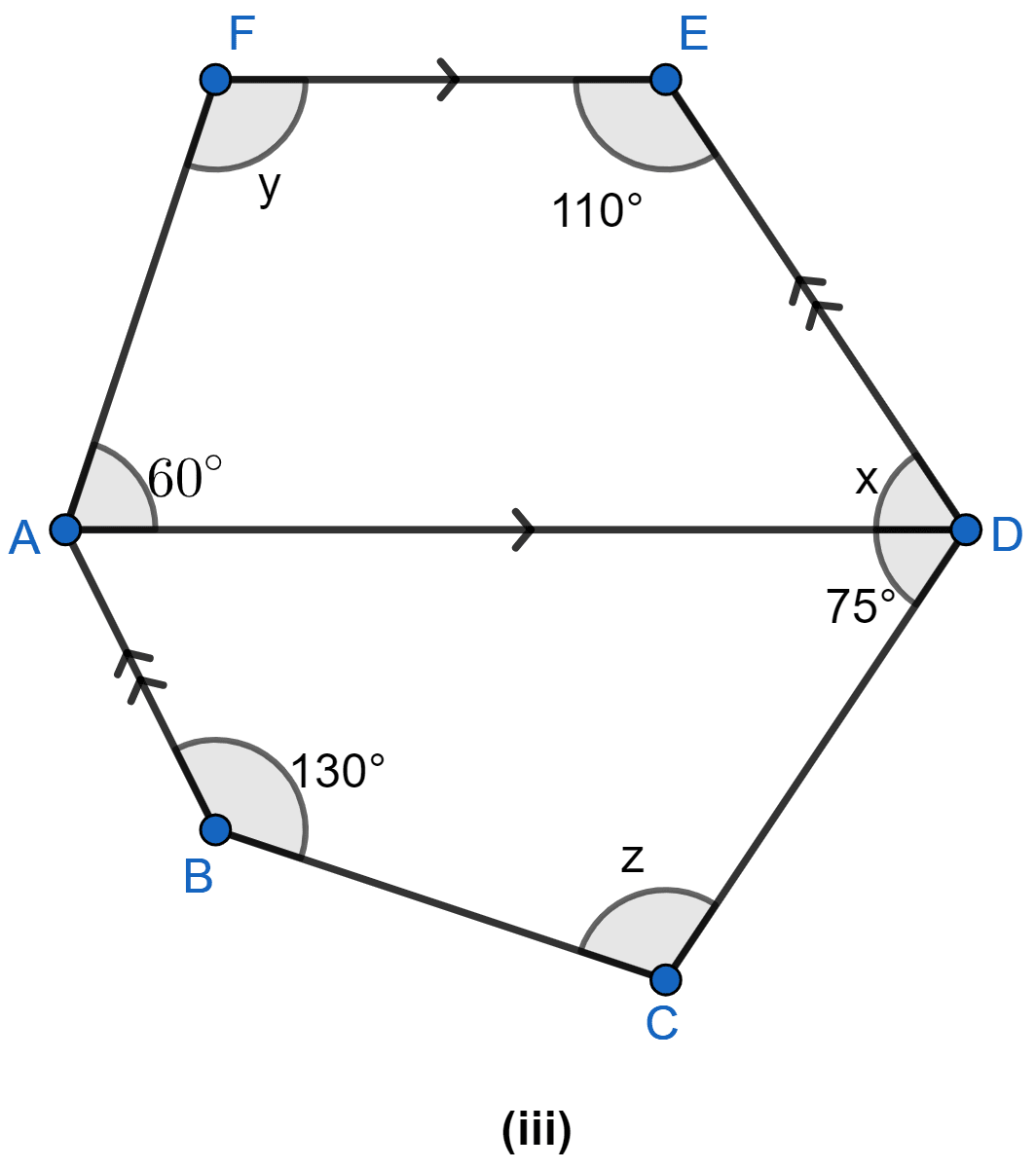
Find the size of each lettered angle in the following figure:
In the adjoining figure, ABCD is a rhombus and DCFE is a square. If ∠ABC = 56°, find
(i) ∠DAG
(ii) ∠FEG
(iii) ∠GAC
(iv) ∠AGC.

If one angle of a rhombus is 60° and the length of a side is 8 cm, find the lengths of its diagonals.