Mathematics
If one angle of a rhombus is 60° and the length of a side is 8 cm, find the lengths of its diagonals.
Rectilinear Figures
24 Likes
Answer
Each side of rhombus ABCD is 8 cm.
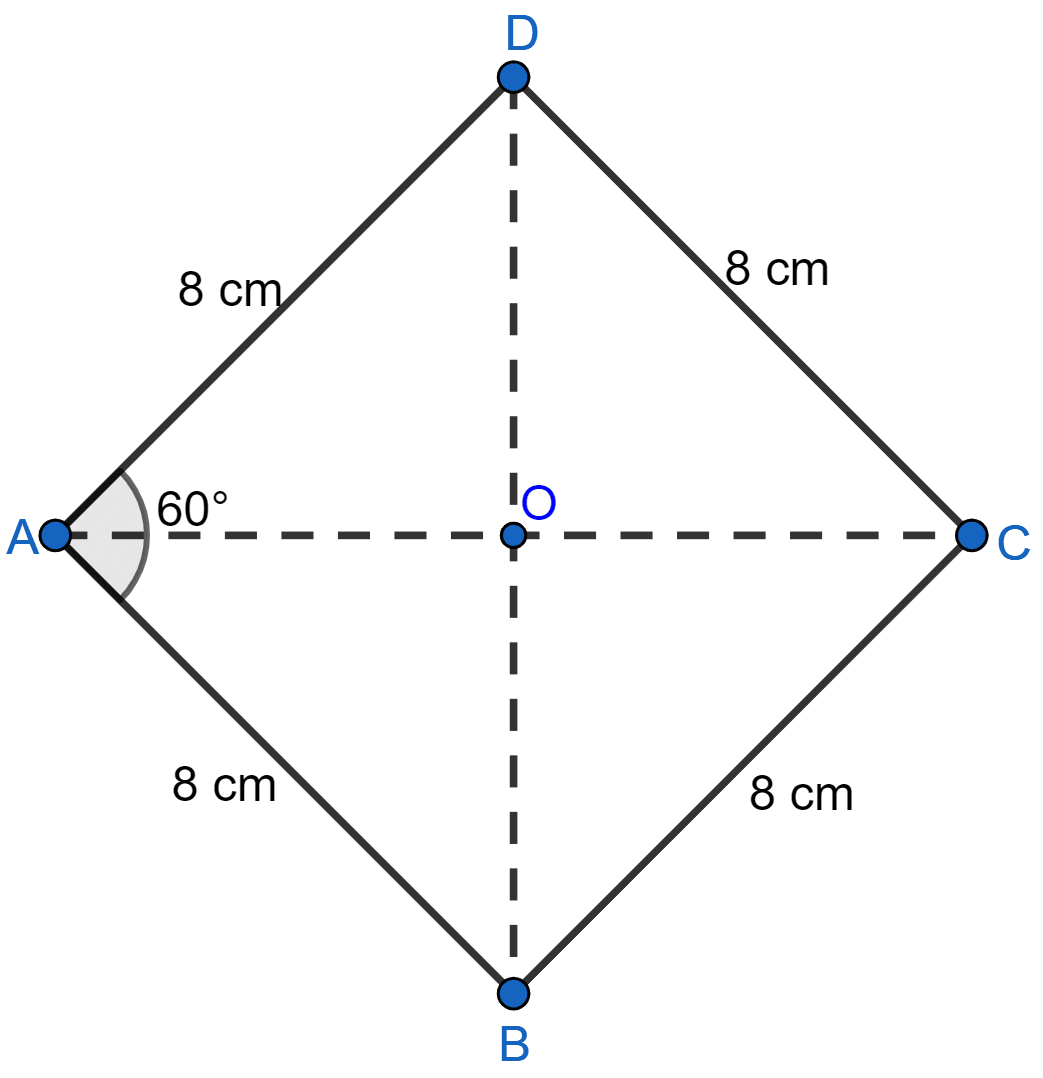
So, AB = BC = CD = DA = 8 cm.
Let ∠A = 60°.
In ∆ABD,
AB = AD
∠ADB = ∠ABD = x (let) (Angles opposite to equal sides are equal.)
⇒ ∠ADB + ∠ABD + ∠DAB = 180°
⇒ x + x + 60° = 180°
⇒ 2x + 60° = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x =
⇒ x = 60°.
Since, all angles = 60°. Hence, △ABD is an equilateral triangle.
So, BD = 8 cm.
As we know, the diagonals of a rhombus bisect each other at right angles
AO = OC, BO = OD = 4cm and ∠AOB = 90°
Now, in right ∆AOB
By Pythagoras theorem,
⇒ AB2 = AO2 + OB2
⇒ 82 = AO2 + 42
⇒ 64 = AO2 + 16
⇒ AO2 = 64 – 16 = 48
⇒ AO = cm.
But, AC = 2AO
⇒ AC = cm.
Hence, length of diagonals = 8 cm and cm.
Answered By
16 Likes
Related Questions
Find the size of each lettered angle in the following figure:

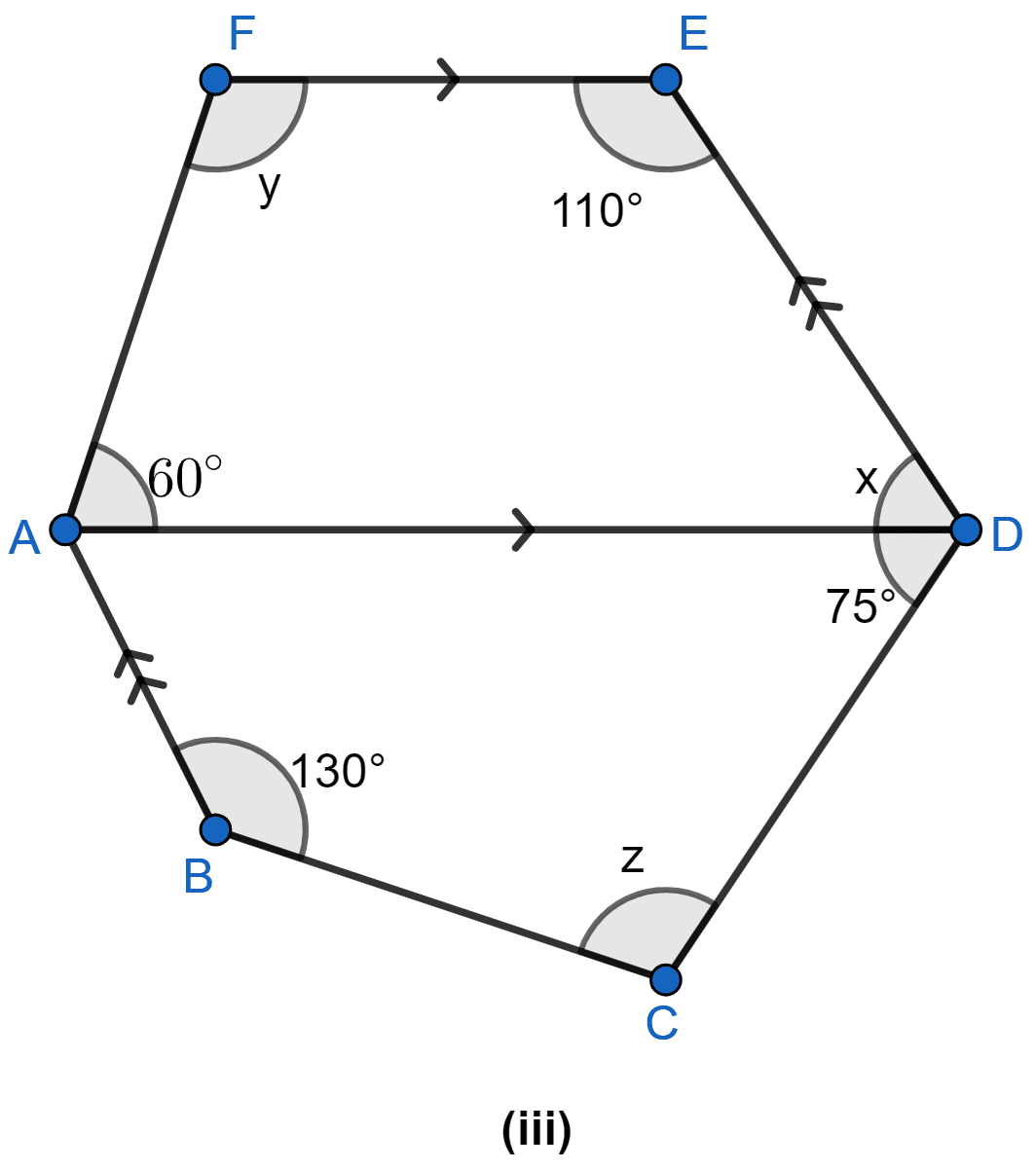
Find the size of each lettered angle in the following figure:
In the adjoining figure, ABCD is a rhombus and DCFE is a square. If ∠ABC = 56°, find
(i) ∠DAG
(ii) ∠FEG
(iii) ∠GAC
(iv) ∠AGC.

Using ruler and compasses only, construct a parallelogram ABCD with AB = 5 cm, AD = 2.5 cm and ∠BAD = 45°. If the bisector of ∠BAD meets DC at E, prove that ∠AEB is a right angle.