Mathematics
Use ruler and compasses only for this question.
(i) Construct △ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
Answer
(i) The constructed triangle is shown below in the figure:
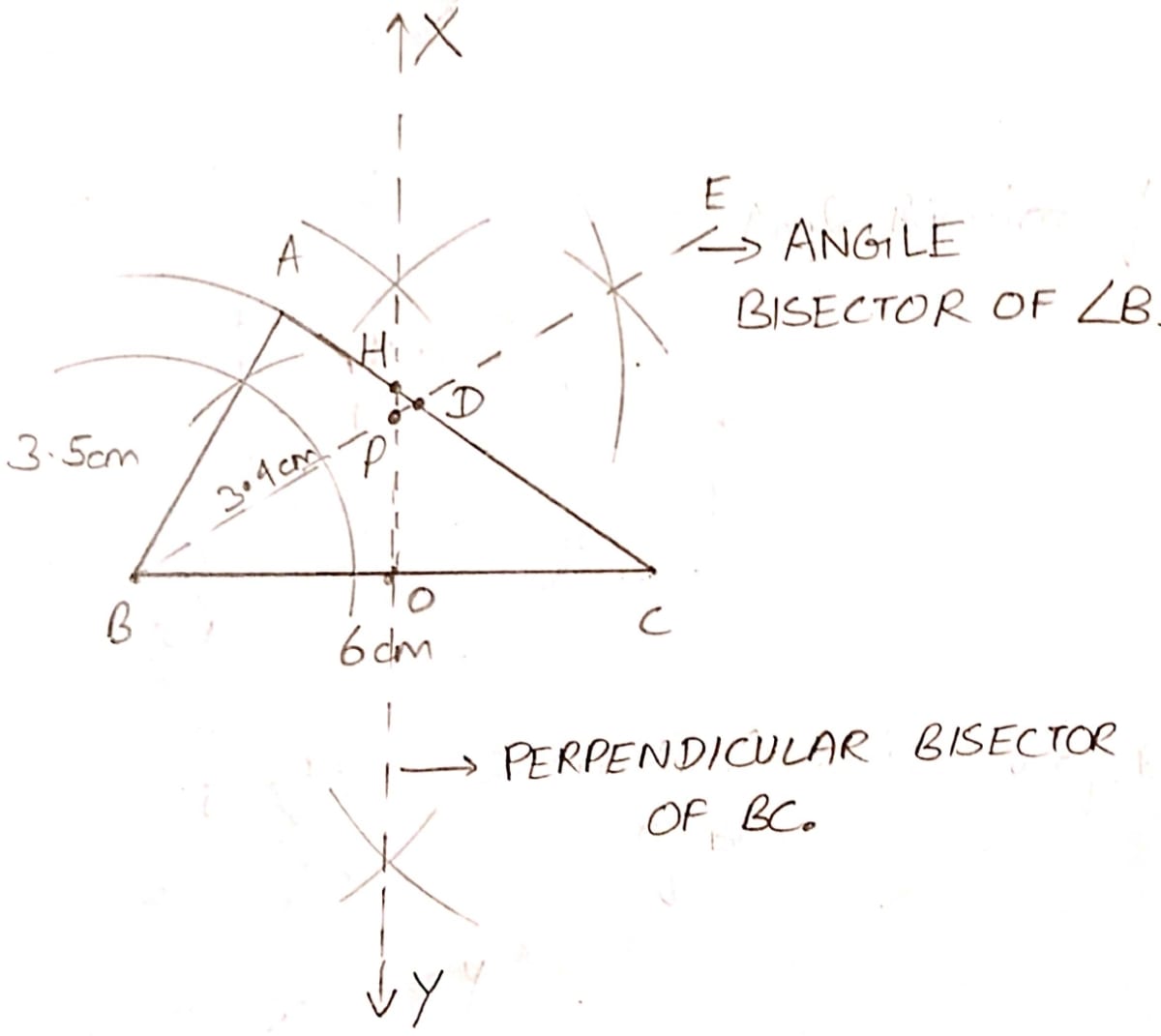
(ii) We know that locus of a point which is equidistant from two lines is the angle bisector between two lines.
From figure,
BE = angle bisector of B, which meets triangle at point D.
Hence, BD is the locus of points inside the triangle which are equidistant from BA and BC.
(iii) We know that locus of a point which is equidistant from two points is the perpendicular bisector joining two points.
From figure,
XY = perpendicular bisector of BC, which meets AC at point H and BC at point O.
Hence, OH is the locus of points inside the triangle which are equidistant from B and C.
(iv) From figure,
Point P is the intersection point of BE and XY. Hence, it is equidistant from AB, BC and also equidistant from B and C.
The length of PB = 3.4 cm.
Related Questions
Construct triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :
(i) P is equidistant from B and C and
(ii) P is equidistant from AB and BC.
(iii) Measure and record the length of PB.
A line segment AB is 8 cm long. Locate by construction the locus of a point which is :
(i) Equidistant from A and B.
(ii) Always 4 cm from the line AB.
(iii) Mark two points X and Y, which are 4 cm from AB and equidistant from A and B. Name the figure AXBY.
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°.
Hence,
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Points A, B and C represent position of three towers such that AB = 60 m, BC = 73 m and CA = 52 m. Taking a scale of 10 m to 1 cm, make an accurate drawing of △ABC. Find by drawing, the location of a point which is equidistant from A, B and C, and its actual distance from any of the towers.