Mathematics
Construct triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :
(i) P is equidistant from B and C and
(ii) P is equidistant from AB and BC.
(iii) Measure and record the length of PB.
Locus
26 Likes
Answer
Construct the △ABC with the given data:
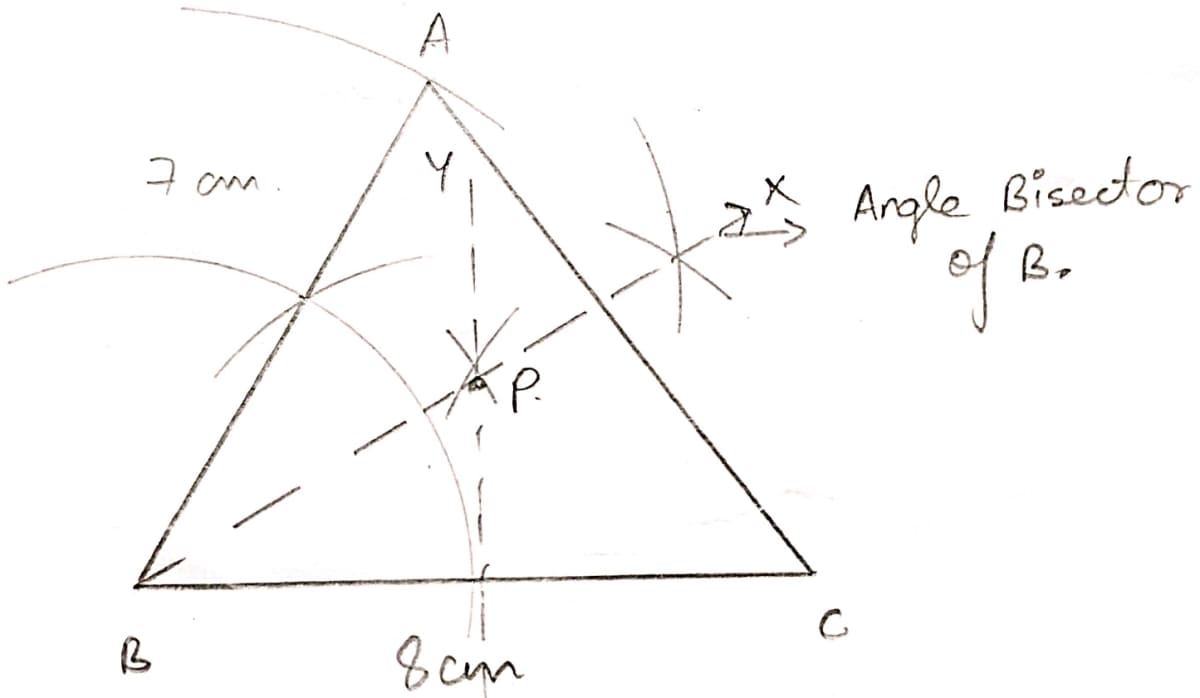
(i) Since, P is equidistant from B and C hence, it will be a point on the perpendicular bisector of BC i.e. YZ.
(ii) Since, P is also equidistant from AB and BC, so, it will be a point on angle bisector of B i.e. BX.
Hence, the intersection of BX and YZ is point P.
(iii) The length of PB is 4.6 cm.
Answered By
15 Likes
Related Questions
Describe completely the locus of centre of a circle of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.
Using ruler and compasses, construct
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of points equidistant from A and C.
Use ruler and compasses only for this question.
(i) Construct △ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.
A line segment AB is 8 cm long. Locate by construction the locus of a point which is :
(i) Equidistant from A and B.
(ii) Always 4 cm from the line AB.
(iii) Mark two points X and Y, which are 4 cm from AB and equidistant from A and B. Name the figure AXBY.