Mathematics
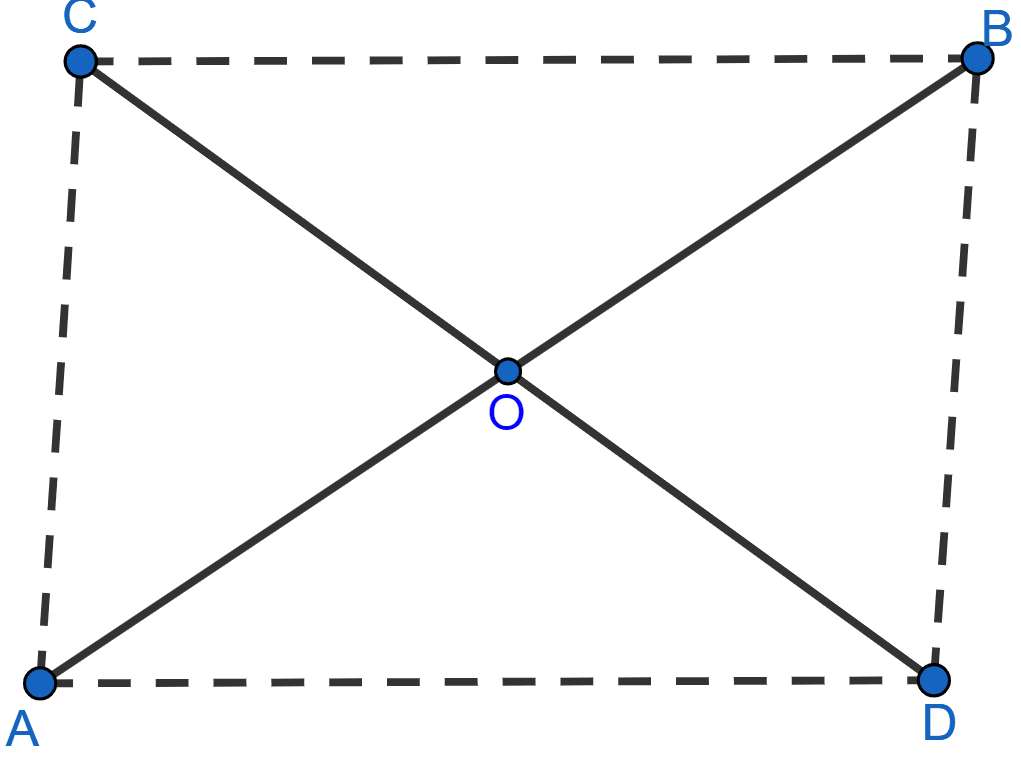
Two line segments AB and CD bisect each other at O. Prove that
(i) AC = BD
(ii) ∠CAB = ∠ABD
(iii) AD || CB
(iv) AD = CB
Answer
(i) Given, AB and CD bisect each other at O.
∴ OC = OD and OA = OB
∠COA = ∠BOD (Vertically opposite angles).
∴ △COA ≅ △BOD by SAS axiom.
We know that corresponding sides of congruent triangles are equal.
Hence, AC = BD.
(ii) As, △COA ≅ △BOD we know that corresponding angles of congruent triangles are equal.
∠CAO = ∠OBD …..(i)
From figure we get,
∠CAO = ∠CAB and ∠OBD = ∠ABD.
Substituting above values in (i) we get,
∠CAB = ∠ABD.
Hence, proved that ∠CAB = ∠ABD.
(iii) From figure,
OC = OD and OA = OB
∠AOD = ∠BOC (Vertically opposite angles).
∴ △COB ≅ △AOD by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ ∠BCO = ∠ADO and ∠CBO = ∠OAD.
Since, ∠BCO, ∠ADO and ∠CBO, ∠OAD are alternate angles,
∴ AD || CB.
Hence, proved that AD || CB.
(iv) Given, AB and CD bisect each other at O.
∴ OC = OD and OA = OB
∠AOD = ∠BOC (Vertically opposite angles).
∴ △AOD ≅ △BOC by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
Hence, AD = CB.
Related Questions
In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) △ACE ≅ △DBF
(ii) AE = DF.

In the adjoining figure, AB = AC and D is the midpoint of BC. Use SSS rule of congruency to show that
(i) △ABD ≅ △ACD
(ii) AD is bisector of ∠A
(iii) AD is perpendicular to BC.

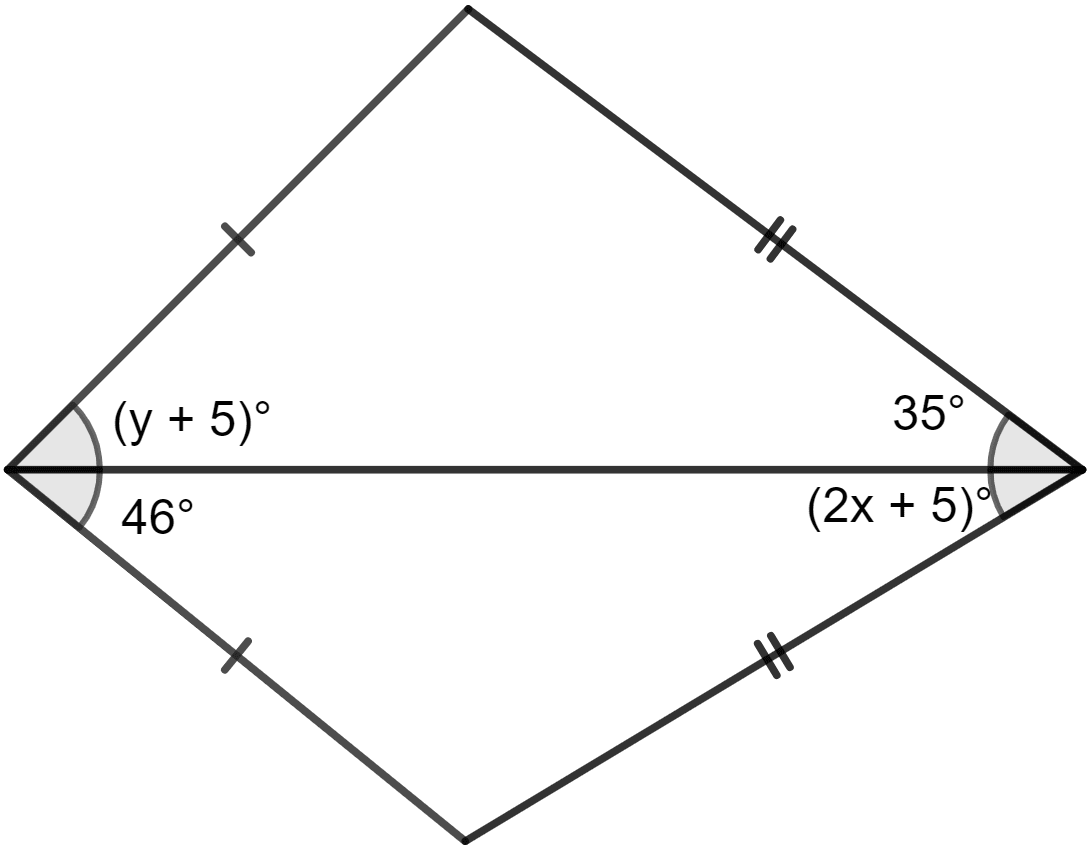
In the adjoining figure, find the values of x and y.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of △PQR should be equal to side AB of △ABC so that the two triangles are congruent? Give reason for your answer.