Two equal cones are touching each other completely at the base circle. Given that the distance between the two vertices is 16 cm and the diameter of the base circle is 12 cm, find the total surface area of this solid.

Given,

Distance between two vertices is 16 cm.

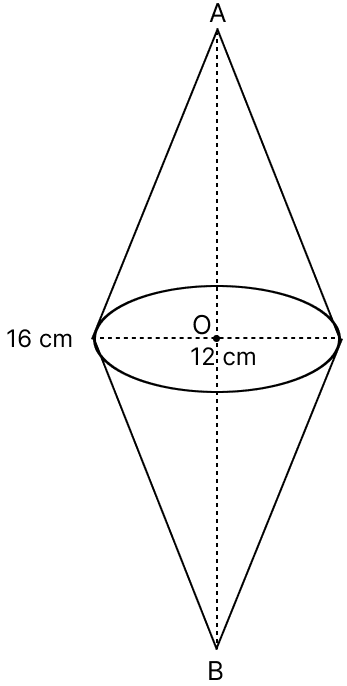
So,

Height of each cone (h) = $\dfrac{16}{2}$ = 8 cm.

Diameter of the base circle = 12 cm

Radius (r) = $\dfrac{12}{2}$ = 6 cm.

From figure,

Surface area of solid = Conical surface area of 1st cone + Conical surface area of 2nd cone

= πrl + πrl

= 2πrl

= $2πr\sqrt{r^2 + h^2}$

Substituting values we get :

$= 2 \times \dfrac{22}{7} \times 6 \times \sqrt{6^2 + 8^2} \\[1em] = \dfrac{264}{7} \times \sqrt{36 + 64} \\[1em] = \dfrac{264}{7} \times \sqrt{100} \\[1em] = \dfrac{264}{7} \times 10 \\[1em] = \dfrac{2640}{7} \\[1em] = 377\dfrac{1}{7} \text{ cm}^2.$

Hence, total surface area of solid = $377\dfrac{1}{7}$ cm².