Mathematics
Two concentric circles are of radii 13 cm and 5 cm. Find the length of the chord of the outer circle which touches the inner circle.
Circles
12 Likes
Answer
From figure,
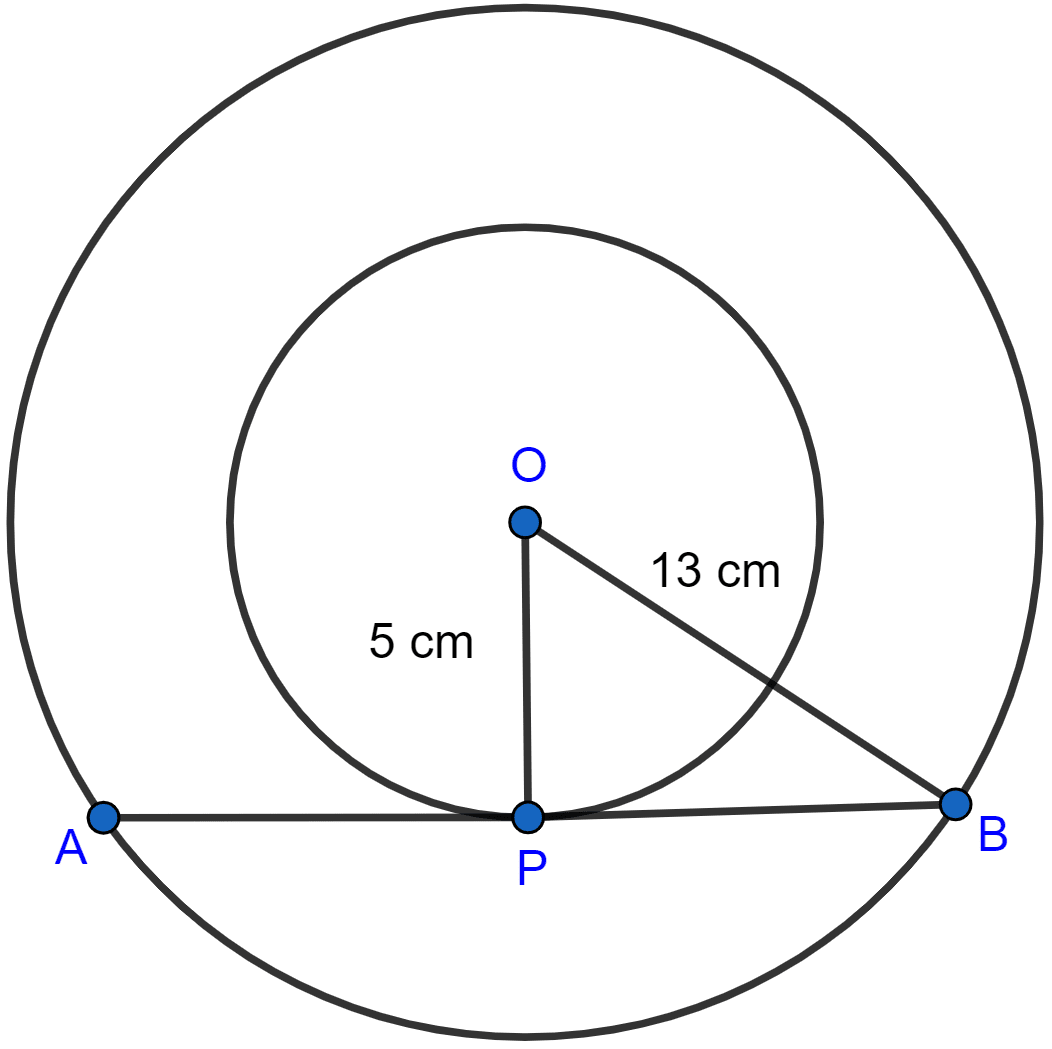
AB is the chord of the outer circle which touches the inner circle at P.
OP is the radius of the inner circle and APB is the tangent to the inner circle.
In the right angled triangle OPB, by pythagoras theorem,
As perpendicular line from centre bisects the chord of the circle so,
AP = PB = 12 cm.
AB = AP + PB = 12 + 12 = 24 cm.
Hence, the length of chord = 24 cm.
Answered By
9 Likes
Related Questions
Two circles of radii 5 cm and 2.8 cm touch each other. Find the distance between their centres if they touch
(i) Externally
(ii) Internally
In figure (i) given below, triangle ABC is circumscribed, find x.

A point P is at a distance 13 cm from the centre C of a circle, and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
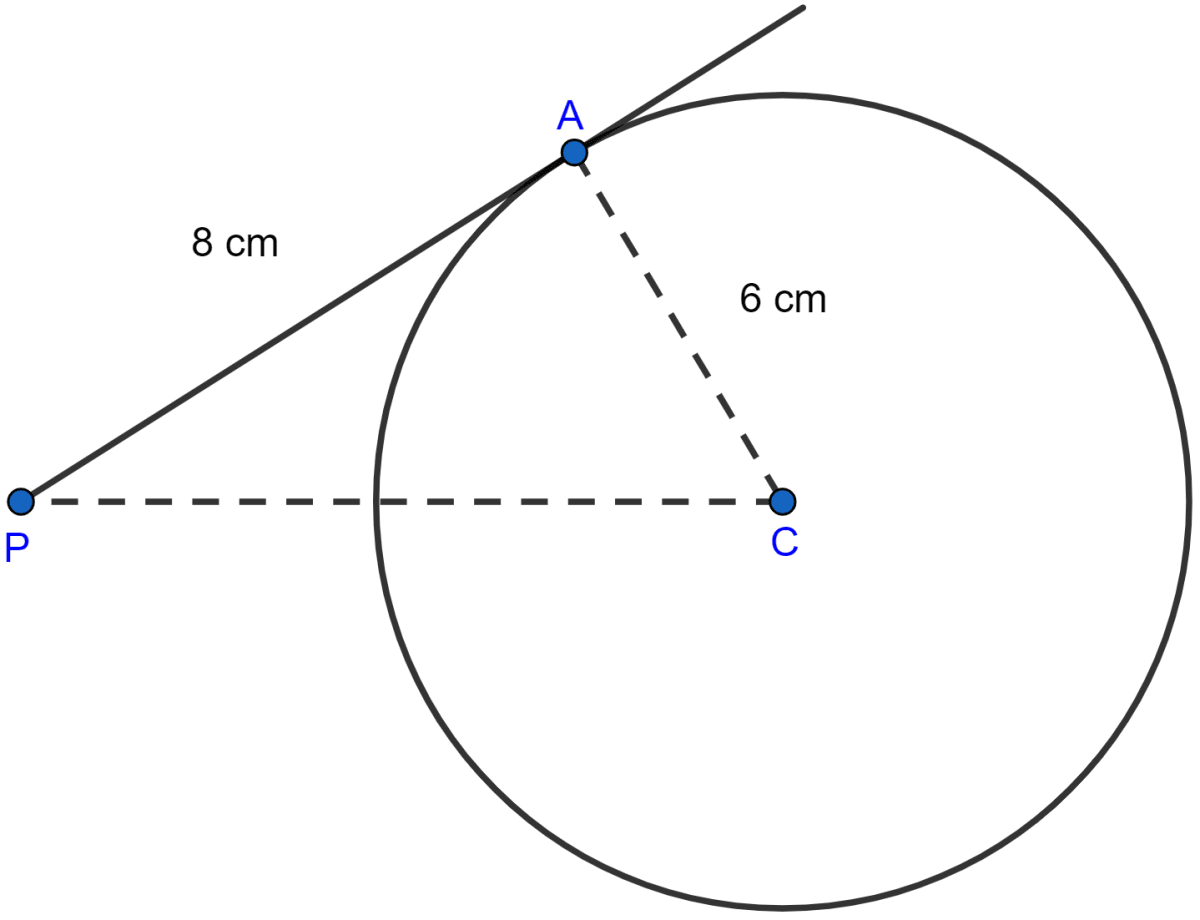
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.