Mathematics
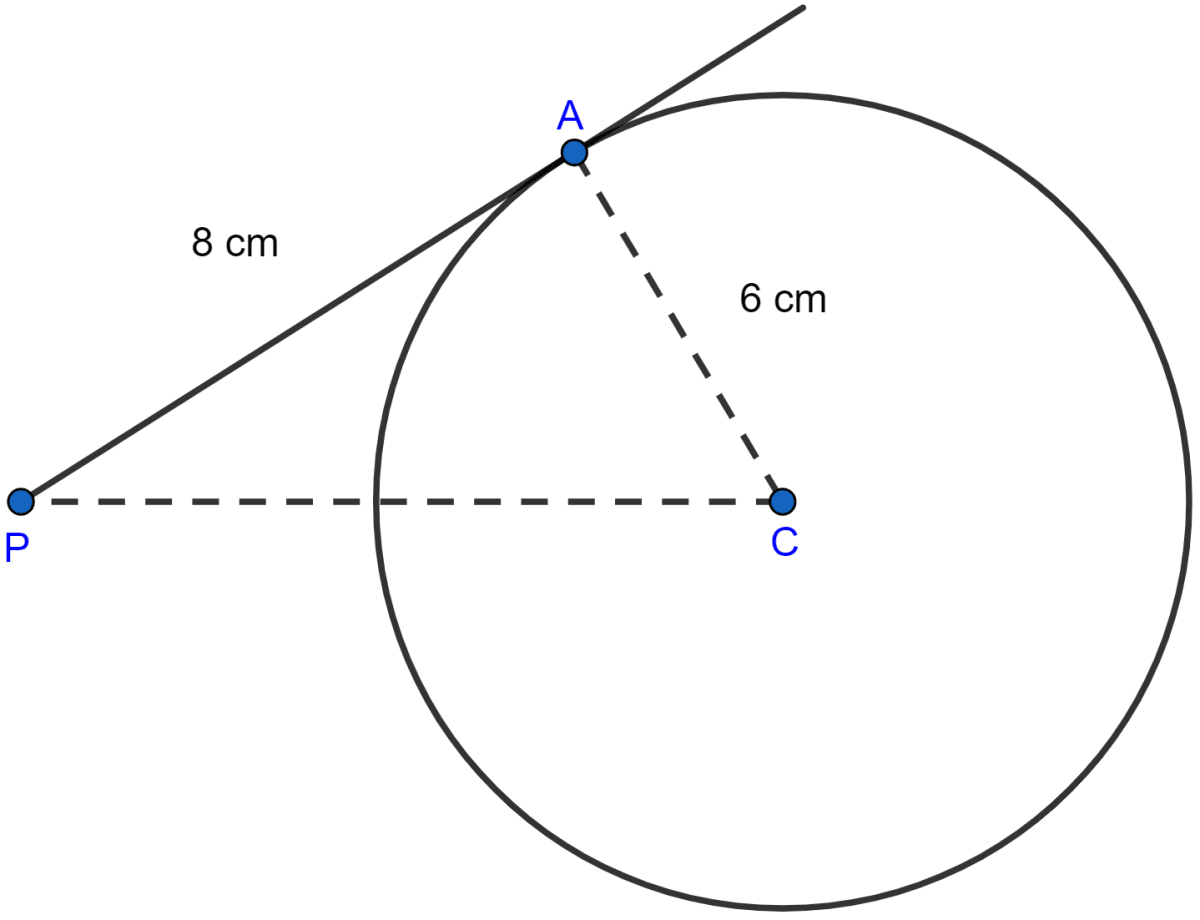
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.
Circles
50 Likes
Answer
Since the tangent at any point of a circle and the radius through the point are perpendicular to each other.
So, from figure,
AP ⊥ CP
So, in right angled △CAP by pythagoras theorem,
From figure, nearest point to P on the circle is D,
PD = CP - CD = 10 - 6 = 4 cm.
Hence, the distance of P from the nearest point of the circle is 4 cm.
Answered By
28 Likes
Related Questions
Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.
A point P is at a distance 13 cm from the centre C of a circle, and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Two concentric circles are of radii 13 cm and 5 cm. Find the length of the chord of the outer circle which touches the inner circle.
Two circles of radii 5 cm and 2.8 cm touch each other. Find the distance between their centres if they touch
(i) Externally
(ii) Internally