Mathematics
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ∠ACP = ∠QCD.
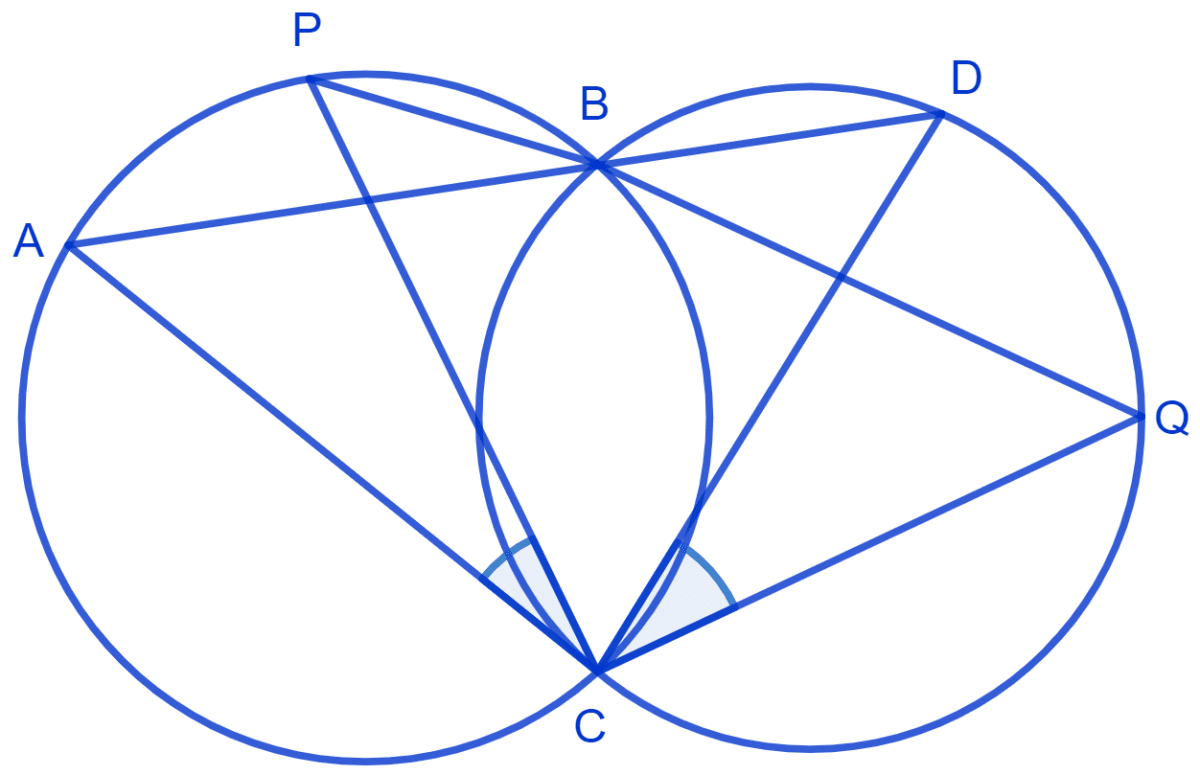
Answer
Join chord AP and DQ.
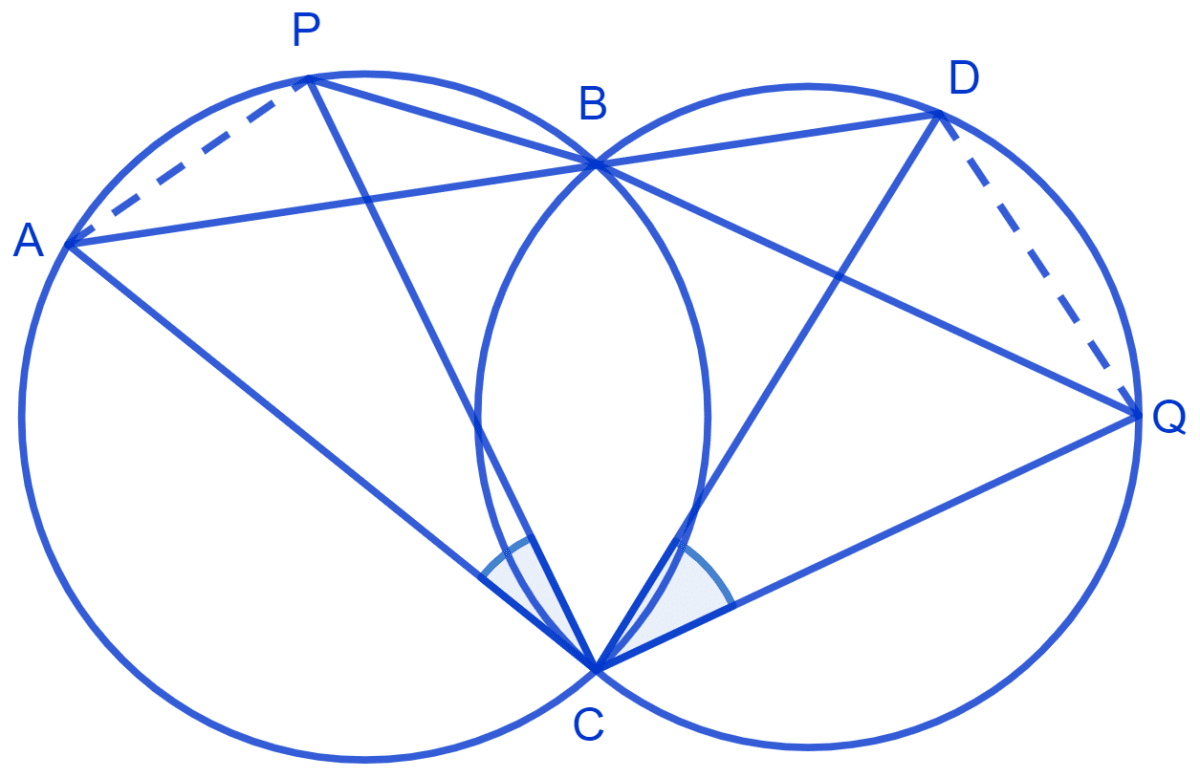
For chord AP,
⇒ ∠PBA = ∠ACP (Angles in the same segment are equal) …..(1)
For chord DQ,
⇒ ∠DBQ = ∠QCD (Angles in the same segment are equal) …..(2)
ABD and PBQ are line segments intersecting at B.
⇒ ∠PBA = ∠DBQ (Vertically opposite angles are equal) ….(3)
From equation (1) and (3) we get :
⇒ ∠DBQ = ∠ACP ………..(4)
From equation (2) and (4) we get :
⇒ ∠QCD = ∠ACP.
Hence, proved that ∠ACP = ∠QCD.
Related Questions
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.