Mathematics
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Circles
3 Likes
Answer
ABCD is a trapezium where AB || DC and AD = BC.
Draw DM and CN perpendicular to AB.
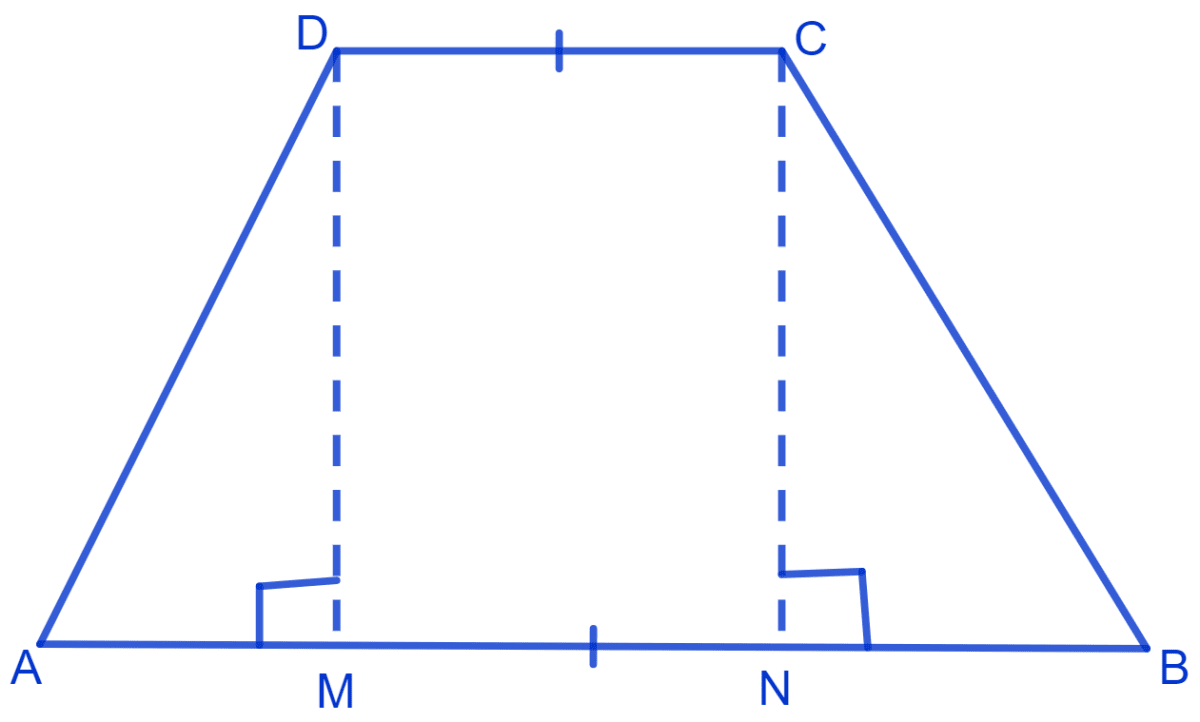
In Δ DAM and Δ CBN,
⇒ AD = BC (Given)
⇒ ∠AMD = ∠BNC (Right angles)
⇒ DM = CN (Perpendicular distance between parallel lines are equal)
∴ ∆ DAM ≅ ∆ CBN, (By R.H.S. congruence rule)
We know that,
Corresponding part of congruent triangle are equal.
⇒ ∠A = ∠B (By C.P.C.T.) …..(1)
From figure,
⇒ ∠B + ∠C = 180° (Sum of the co-interior angles = 180°)
Substituting value of ∠B from equation (1) in above equation, we get :
⇒ ∠A + ∠C = 180°
We know that,
Sum of angles in a quadrilateral = 360°.
∴ ∠A + ∠B + ∠C + ∠D = 360°
⇒ (∠A + ∠C) + (∠B + ∠D) = 360°
⇒ 180° + (∠B + ∠D) = 360°
⇒ (∠B + ∠D) = 360° - 180°
⇒ (∠B + ∠D) = 180°.
ABCD is a cyclic quadrilateral as the sum of the pair of opposite angle is 180°.
Hence, if the non-parallel sides of a trapezium are equal, it is cyclic.
Answered By
1 Like
Related Questions
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
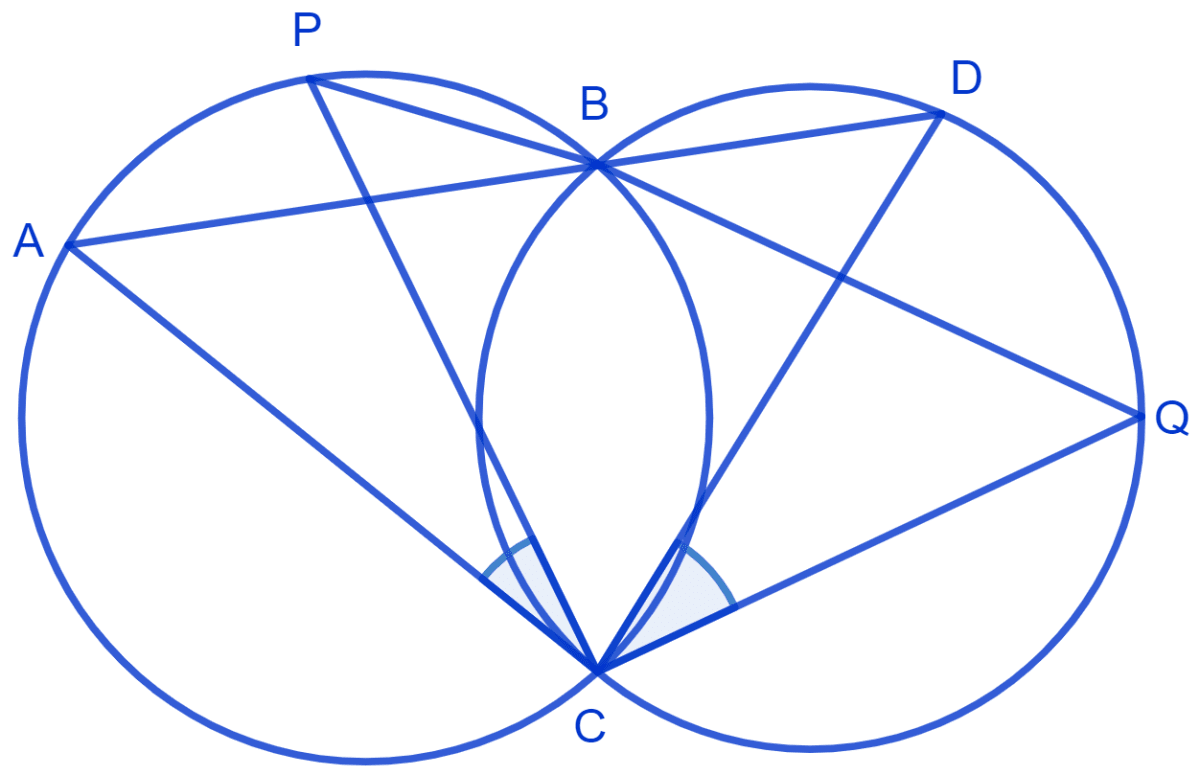
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ∠ACP = ∠QCD.
