Mathematics
Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, prove that AB = CD.
Answer
We know that when two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
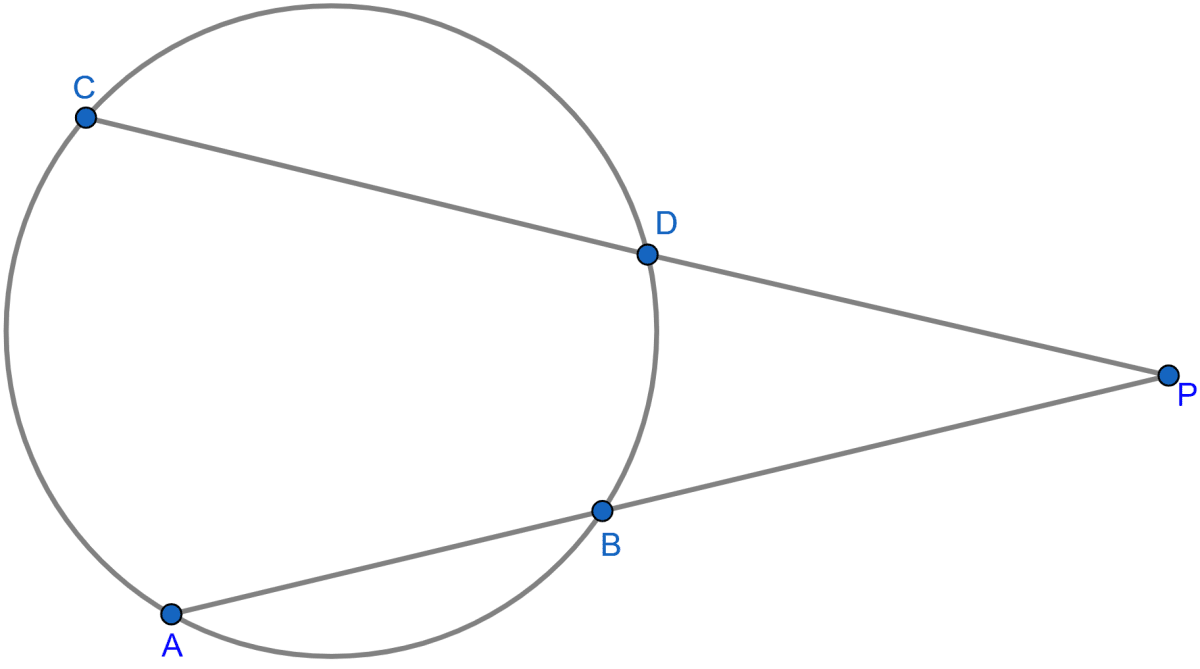
Given, chords AB and CD of a circle intersect externally at a point P. So,
PA.PB = PC.PD …..(Eq. 1)
Let PA = a, so PC = a. (∵ PA = PB)
Putting these value in Eq. 1 we get,
a.PB = a.PD
Dividing both sides by a we get,
PB = PD.
Let PB = PD = b
From figure,
AB = PA - PB = a - b.
CD = PC - PD = a - b.
Hence, proved that AB = CD.
Related Questions
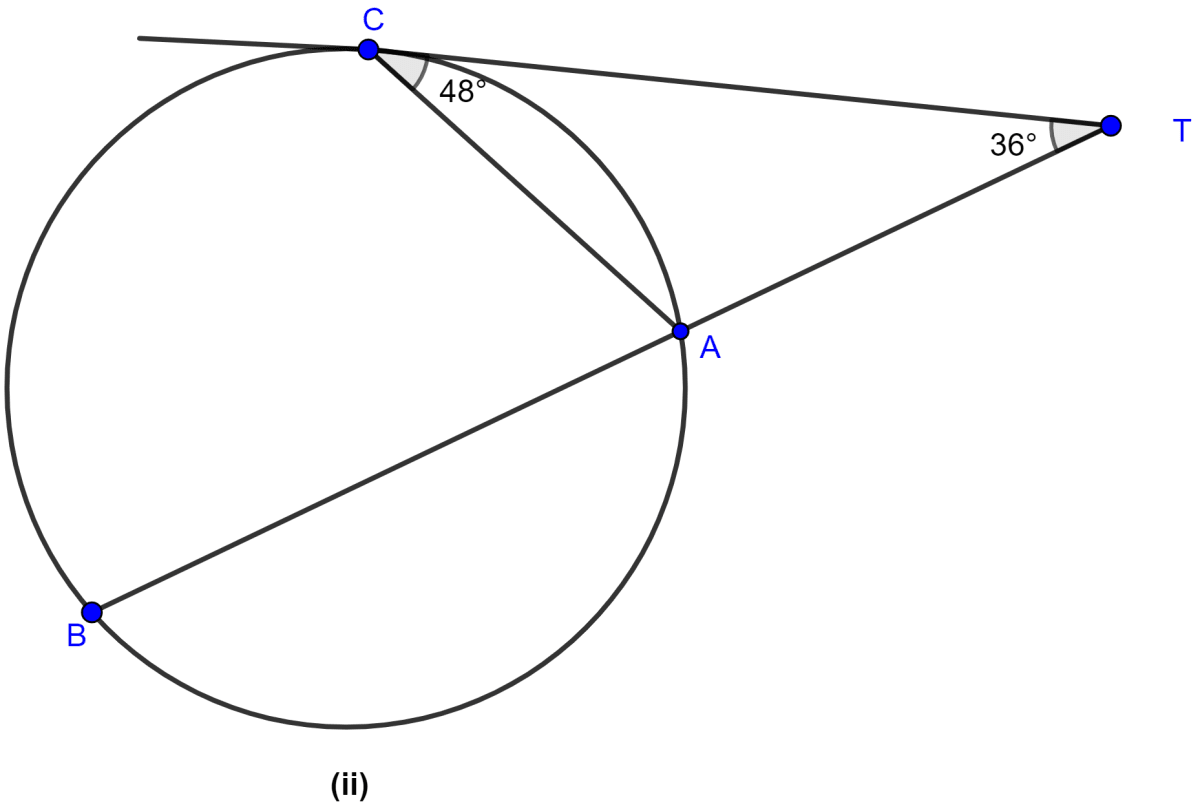
In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle.
In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.

In the figure (i) given below, PAB is a secant and PT is tangent to a circle. If PA : AB = 1 : 3 and PT = 6 cm, find the length of PB.

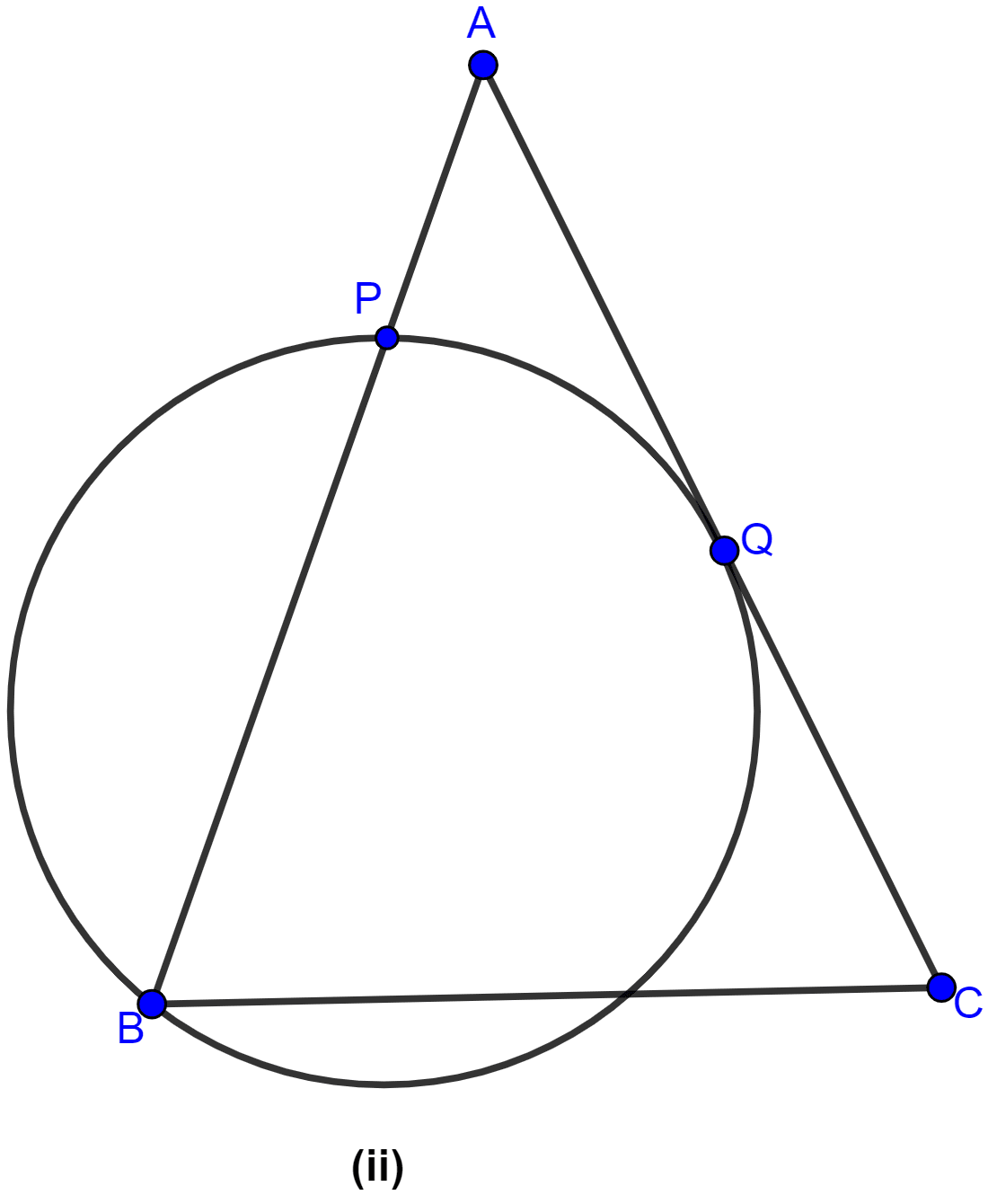
In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant and AC is tangent to the circle at Q, prove that AB = 4AP.