Physics
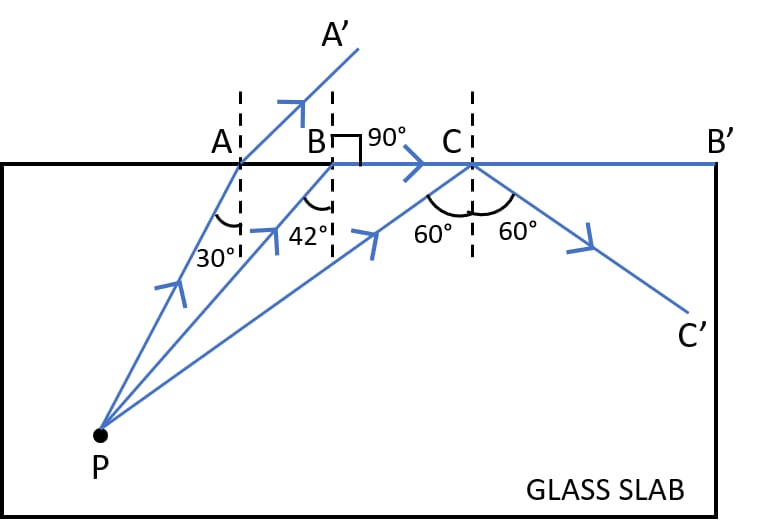
The refractive index of glass is 1.5. From a point P inside a glass slab, draw rays PA, PB and PC incident on the glass-air surface at an angle of incidence 30°, 42° and 60° respectively.
(a) In the diagram show the approximate direction of these rays as they emerge out of the slab.
(b) What is the angle of refraction for the ray PB?
(Take sin 42° = 2 / 3)
Refraction Plane Surfaces
45 Likes
Answer
(a) Diagram with rays PA, PB and PC is shown below:
(b) Given,
μg = 1.5
As we know,
Substituting the values in the formula we get,
c = \dfrac{1}{1.5} \\[0.5em] \Rightarrow \text {sin i}c = 0.667 \\[0.5em] \Rightarrow i_c = 41.8
Hence, we can round off ic = 42°
Applying,
a\mug \\[0.5em] \text {sin r} = a\mug \times \text {sin i} \\[0.5em] \text {sin r} = a\mug × \text {sin 42°} \\[0.5em]
Given,
and
aμg = \dfrac{3}{2}
Substituting the values in the formula we get,
As sin r = 1 , so angle of refraction = 90°.
Answered By
29 Likes
Related Questions
Figure shows a point source P inside a water container. Three rays A, B and C starting from the source P are shown up to the water surface.
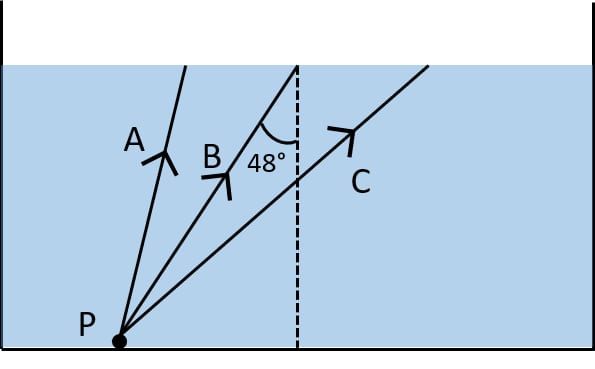
(a) Show in the diagram, the path of these rays after striking the water surface. The critical angle for water-air surface is 48°.
(b) Name the phenomenon which the rays A, B and C exhibit.
In the figure, PQ and PR are the two light rays emerging from an object P. The ray PQ is refracted as QS.
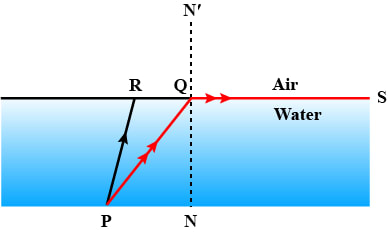
(a) State the special name given to the angle of incidence ∠PQN of the ray PQ.
(b) What is the angle of refraction for the refracted ray QS?
(c) Name the phenomenon that occurs if the angle of incidence ∠PQN is increased.
(d) The ray PR suffers partial reflection and refraction on the water-air surface. Give reason.
(e) Draw in the diagram the refracted ray for the incident ray PR and hence show the position of image of the object P by the letter P' when seen vertically from above.
A ray of light enters a glass slab ABDC as shown in figure and strikes at the centre O of the circular part AC of the slab. The critical angle of glass is 42°. Complete the path of the ray till it emerges out from the slab. Mark the angles in the diagram wherever necessary.

What is a total reflecting prism? State three actions that it can produce. Draw a diagram to show one such action of the total reflecting prism.