The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate :

(i) the length of AB;

(ii) the distance of AB from the centre C.

Given,

CA = CB = 15 cm and ∠ACB = 131°.

Construct a perpendicular CP from center C to the chord AB.

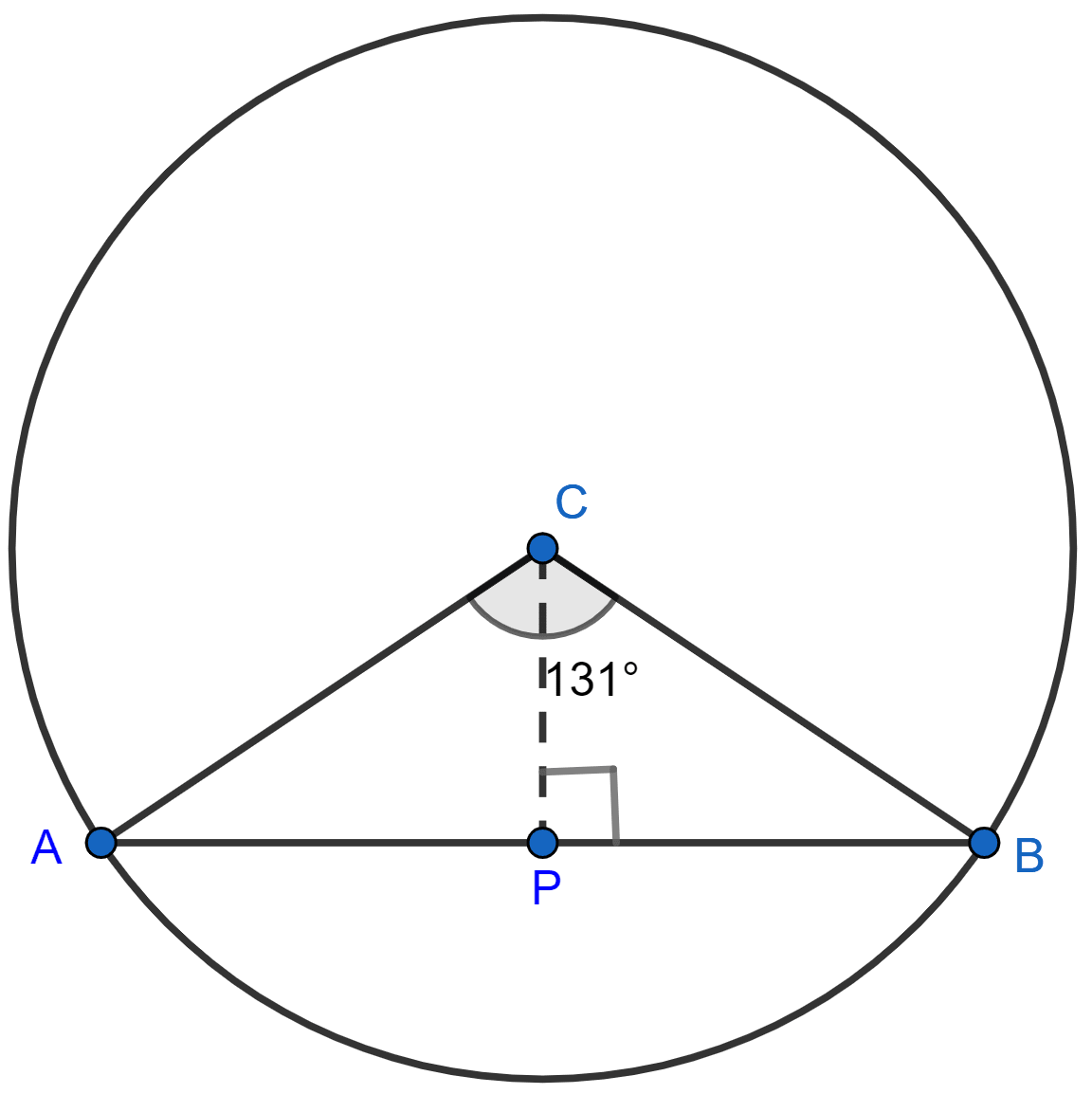
We know that perpendicular form center to the chord bisects the chord.

Then, CP bisects AB.

In △ACP and △BCP,

∠APC = ∠BPC = 90°

CP = CP [∵ Common Side]

AP = PB [∵ CP bisects AB]

∴ △ACP ≅ △BCP by SAS axiom.

∴ ∠ACP = ∠BCP = $\dfrac{131°}{2}$ = 65.5° [By C.P.C.T.]

In △ACP,

$\text{sin 65.5°} = \dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \\[1em] \Rightarrow 0.91 = \dfrac{AP}{AC} \\[1em] \Rightarrow AP = 0.91 \times AC \\[1em] \Rightarrow AP = 0.91 \times 15 = 13.65 \text{ cm}.$

(i) From figure,

AB = AP + PB = 2AP

= 2 × 13.65

= 27.30 cm

Hence, AB = 27.30 cm.

(ii) In △ACP,

$\text{cos 65.5°} = \dfrac{\text{Base}}{\text{Hypotenuse}} \\[1em] \Rightarrow 0.415 = \dfrac{CP}{AC} \\[1em] \Rightarrow CP = 0.415 \times 15 \\[1em] \Rightarrow CP = 6.225 \text{ cm}.$

Hence, CP = 6.225 cm.