Mathematics
The point (-3, 0) on reflection in a line is mapped as (3, 0) and the point (2, -3) on reflection in the same line is mapped as (-2, -3).
(i) Name the mirror line.
(ii) Write the coordinates of the image of (-3, -4) in the mirror line.
Answer
Given, the point (-3, 0) is the image of point (3, 0) and (-2, -3) is the image of point (2, -3) in the same line.
Considering graph,
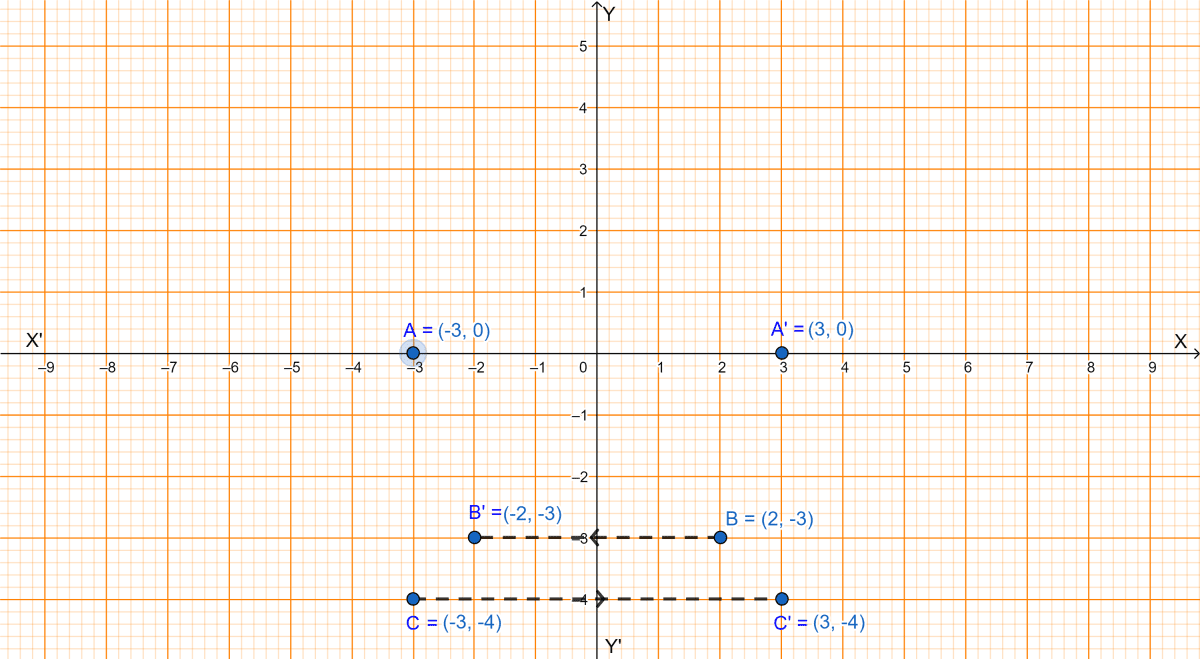
(i) The mirror line is y-axis.
(ii) Since, the mirror line is y-axis. We know that,
Rule to find reflection of a point in y-axis :
- Change the sign of abscissa i.e. x-coordinate.
- Retain the ordinate i.e. y-coordinate.
Let C be the point (-3, -4).
∴ C' (3, -4) is the image on reflection of C (-3, -4) in y-axis.
Hence, the reflection of (-3, -4) in y-axis is (3, -4).
Related Questions
The image of a point P on reflection in a line l is a point P'. Describe the location of the line l.
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate (i) the x-axis (ii) the y-axis and (iii) the origin.
Use graph paper for this question (take 2cm = 1 unit along both x and y axis). ABCD is a quadrilateral whose vertices are A(2, 2), B(2, -2), C(0, -1) and D(0, 1).
(i) Reflect quadrilateral ABCD on the y-axis and name it as A'B'CD.
(ii) Write down the coordinates of A' and B'.
(iii) Name two points which are invariant under the above reflection.
(iv) Name the polygon A'B'CD.
Use a graph sheet for this question. Take 1cm = 1 unit along both x and y-axes.
(i) Plot the points : A(0, 5), B(3, 0), C(1, 0) and D(1, -5).
(ii) Reflect the points B, C and D on the y-axis and name them as B', C' and D' respectively.
(iii) Write down the coordinates of B', C' and D'.
(iv) Join the points A, B, C, D, D', C', B', A in order and give a name to the closed figure ABCDD'C'B'.