The parallel sides of an isosceles trapezium are in the ratio 2 : 3. If its height is 4 cm and area is 60 cm², find the perimeter.

Since, ABCD is an isosceles trapezium so, BC = AD.

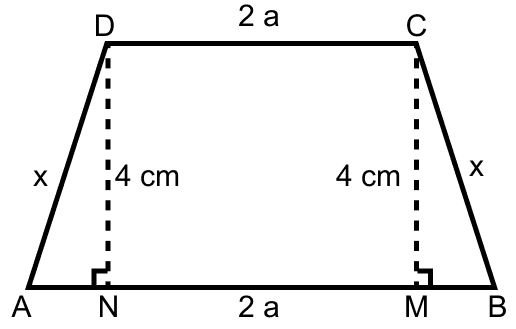
Since, parallel sides of an isosceles trapezium are in the ratio 2 : 3.

∴ CD = 2a and AB = 3a.

Construct perpendicular DN from D to AB and perpendicular CM from C to AB.

Given,

Area = 60 cm²

By formula,

Area of trapezium = $\dfrac{1}{2}$ × sum of parallel sides × height

⇒ 60 = $\dfrac{1}{2}$ × (AB + DC) × DN

⇒ 60 = $\dfrac{1}{2}$ × (3a + 2a) × 4

⇒ 60 = 2 × 5a

⇒ 10a = 60

⇒ a = 6 cm.

⇒ AB = 3a = 3 × 6 = 18 cm and CD = 2a = 2 × 6 = 12 cm.

In △ADN and △BCM,

⇒ ∠AND = ∠CMB = 90°

⇒ DN = CM = 4 cm

⇒ AD = CB = x cm (let) (As ABCD is an isosceles trapezium).

∴ △ADN ≅ △BCM by RHS axiom.

∴ AN = MB ……..(1)

Since, DNMC is a rectangle.

∴ NM = DC = 12 cm. (As opposite sides of a rectangle are equal.)

From figure,

⇒ AN + NM + MB = 18

⇒ AN + 12 + MB = 18

⇒ AN + MB = 6

⇒ 2AN = 6 (As AN = MB)

⇒ AN = $\dfrac{6}{2}$ = 3 cm.

⇒ MB = 3 cm.

In right angle triangle AND,

⇒ AD² = AN² + DN²

⇒ x² = 4² + 3²

⇒ x² = 16 + 9

⇒ x² = 25

⇒ x = $\sqrt{25}$ = 5 cm.

From figure,

Perimeter = AB + BC + CD + DA

= 18 + 5 + 12 + 5

= 40 cm.

Hence, perimeter of trapezium = 40 cm.