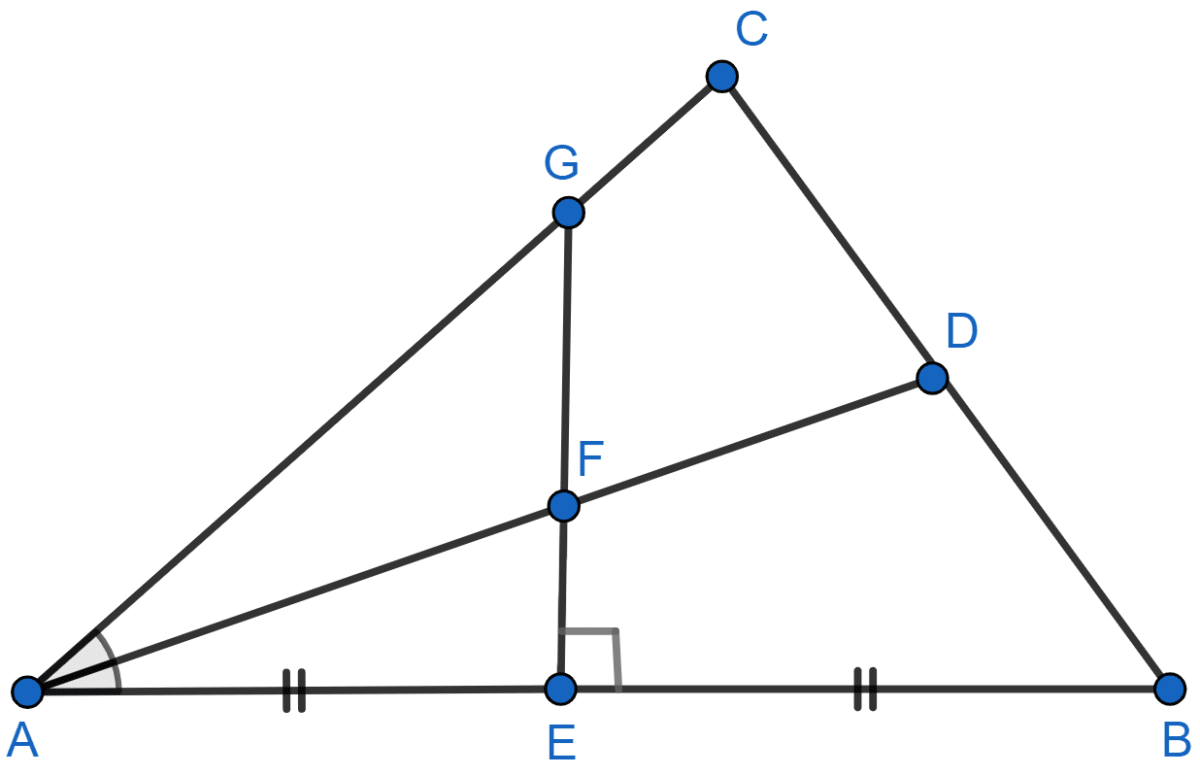
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F. Prove that :

(i) F is equidistant from A and B.

(ii) F is equidistant from AB and AC.

(i) Construct FB.

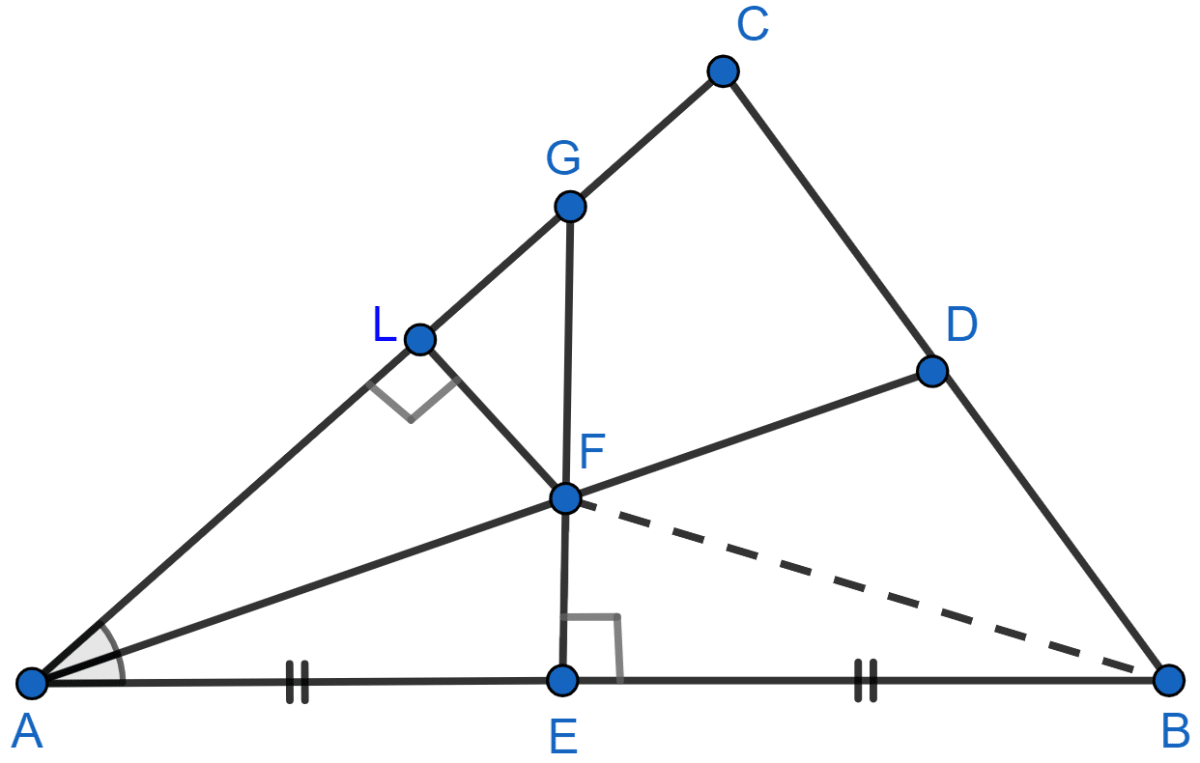
In △FAE and △FBE,

⇒ ∠FEA = ∠FEB [Both equal to 90°]

⇒ FE = FE [Common]

⇒ AE = EB [Given]

∴ △FAE ≅ △FBE by SAS axiom.

∴ FA = FB [By C.P.C.T.]

Hence, proved that F is equidistant from A and B.

(ii) Draw FL ⊥ AC.

In △FAL and △FAE,

⇒ ∠FLA = ∠FEA [Both equal to 90°]

⇒ FA = FA [Common]

⇒ ∠LAF = ∠FAE [Since, AD bisects ∠BAC]

∴ △FAL ≅ △FAE by AAS axiom.

∴ FL = FE [By C.P.C.T.]

Hence, proved that F is equidistant from AB and AC.