Mathematics
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = x - 1. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
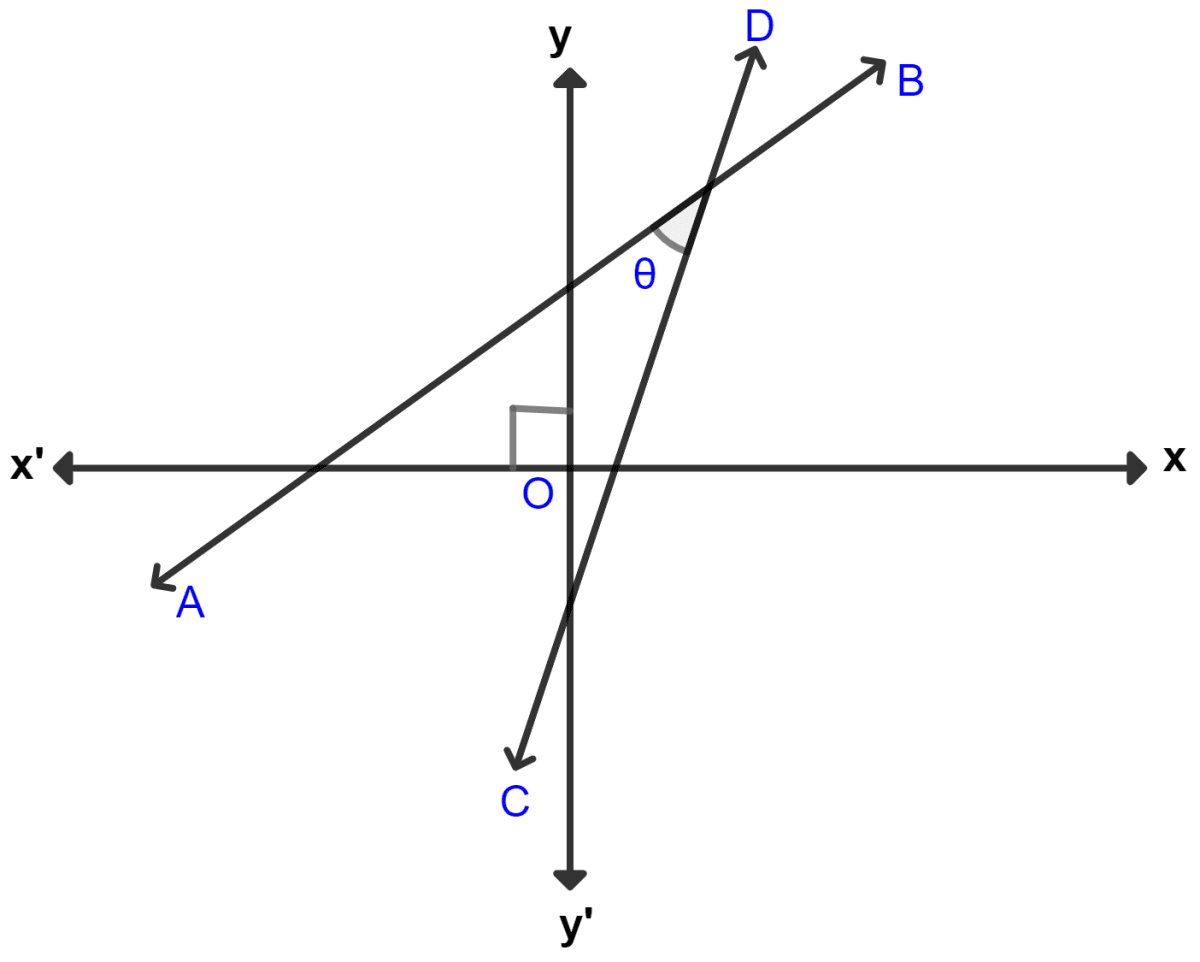
Straight Line Eq
4 Likes
Answer
Given,
Equation of AB :
⇒ y = x + 1
Comparing the above equation with y = mx + c we get,
Slope of AB = 1.
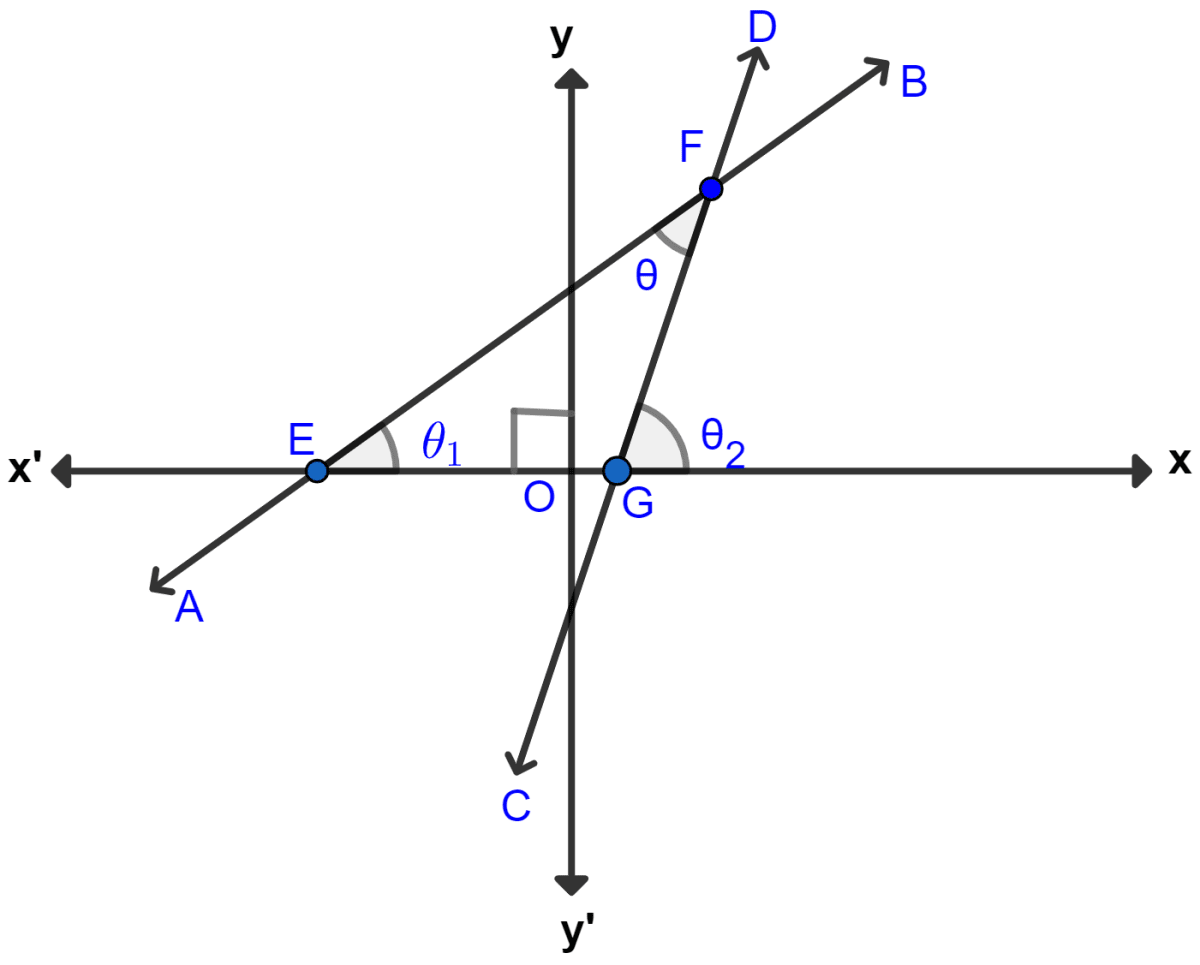
Let θ1 be the inclination of AB then,
⇒ tan θ1 = 1
⇒ tan θ1 = tan 45°
⇒ θ1 = 45°.
Equation of CD :
⇒ y = x - 1
Comparing the above equation with y = mx + c we get,
Slope of CD = .
Let θ2 be the inclination of AB then,
⇒ tan θ2 =
⇒ tan θ2 = tan 60°
⇒ θ2 = 60°.
From figure,
∠FGE = 180° - θ2 = 180° - 60° = 120°.
In △EFG,
∠E + ∠F + ∠G = 180
⇒ θ1 + θ + 120° = 180°
⇒ 45° + θ + 120° = 180°
⇒ θ + 165° = 180°
⇒ θ = 180° - 165° = 15°.
Hence, inclination of AB is 45°, inclination of CD is 60° and θ = 15°.
Answered By
3 Likes
Related Questions
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
The ordinate of a point lying on the line joining the points (6, 4) and (7, -5) is -23. Find the co-ordinates of that point.
Write down the equation of the line whose gradient is and which passes through P, where P divides the line segment joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
A line intersects x-axis at point (-2, 0) and cuts off an intercept of 3 units from the positive side of y-axis. Find the equation of the line.