Mathematics
Write down the equation of the line whose gradient is and which passes through P, where P divides the line segment joining A(-2, 6) and B(3, -4) in the ratio 2 : 3.
Straight Line Eq
4 Likes
Answer
By section-formula,
P = 1x2 + m2x1}{m1 + m2}, \dfrac{m1y2 + m2y1}{m1 + m2}\Big)
Substituting values we get,
By point-slope form,
Equation of line with slope = and passing through (0, 2) is :
⇒ y - y1 = m(x - x1)
⇒ y - 2 = (x - 0)
⇒ 2(y - 2) = 3x
⇒ 2y - 4 = 3x
⇒ 2y = 3x + 4.
Hence, equation of required line is 2y = 3x + 4.
Answered By
3 Likes
Related Questions
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units.
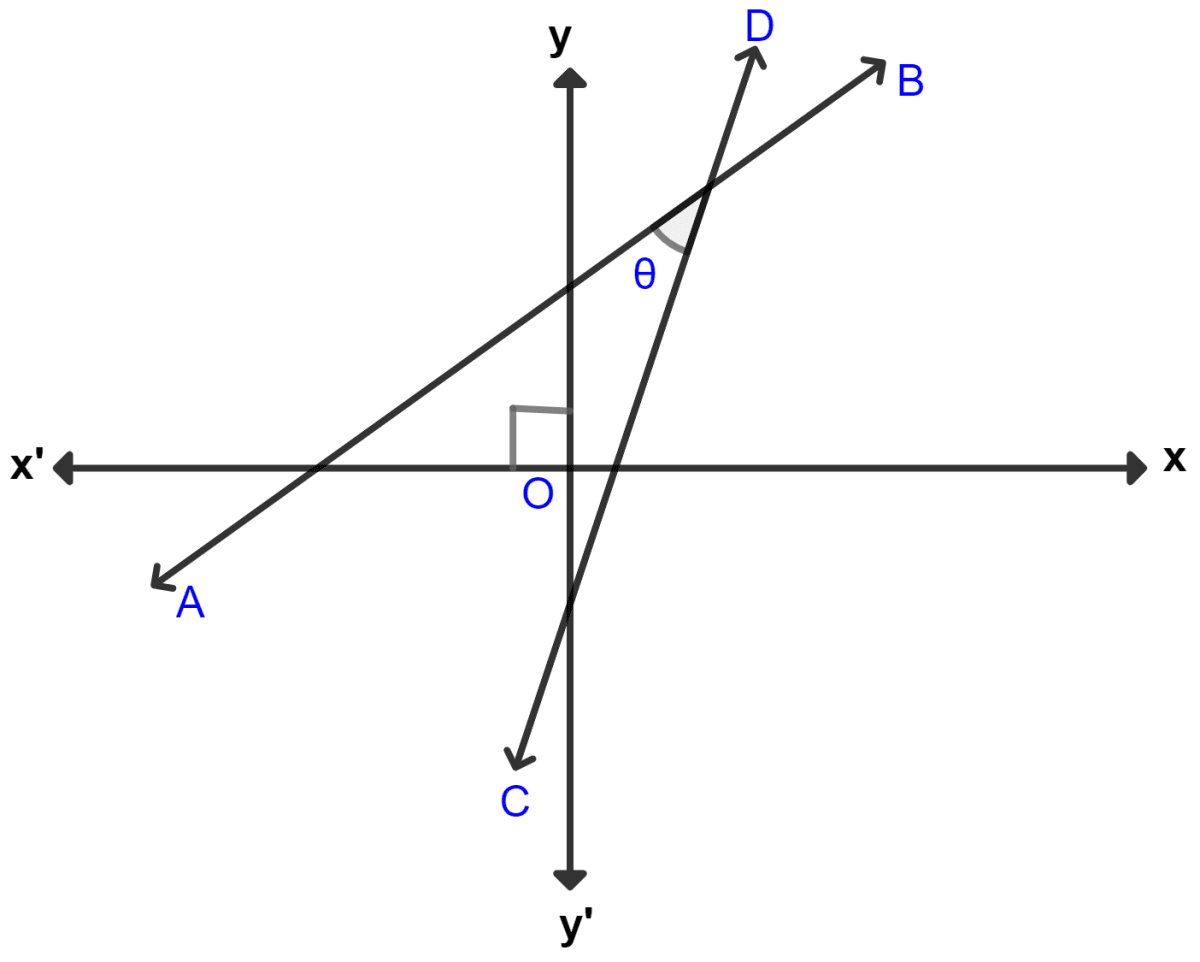
The given figure (not drawn to scale) shows two straight lines AB and CD. If equation of the line AB is : y = x + 1 and equation of line CD is : y = x - 1. Write down the inclination of lines AB and CD; also, find the angle θ between AB and CD.
The ordinate of a point lying on the line joining the points (6, 4) and (7, -5) is -23. Find the co-ordinates of that point.
Point A and B have co-ordinates (7, -3) and (1, 9) respectively. Find :
(i) the slope of AB.
(ii) the equation of perpendicular bisector of the line segment AB.
(iii) the value of 'p' if (-2, p) lies on it.