The fourth vertex D of a parallelogram ABCD whose vertices are A(-2, 3), B(6, 7) and C(8, 3) is

1. (0, 1)

2. (0, -1)

3. (-1, 0)

4. (1, 0)

ABCD is a parallelogram whose three vertices are A(-2, 3), B(6, 7) and C(8, 3). Let coordinates of its fourth vertex D be (x, y).

The diagonals AC and BD bisect each other at O so O is the mid-point of AC as well as BD.

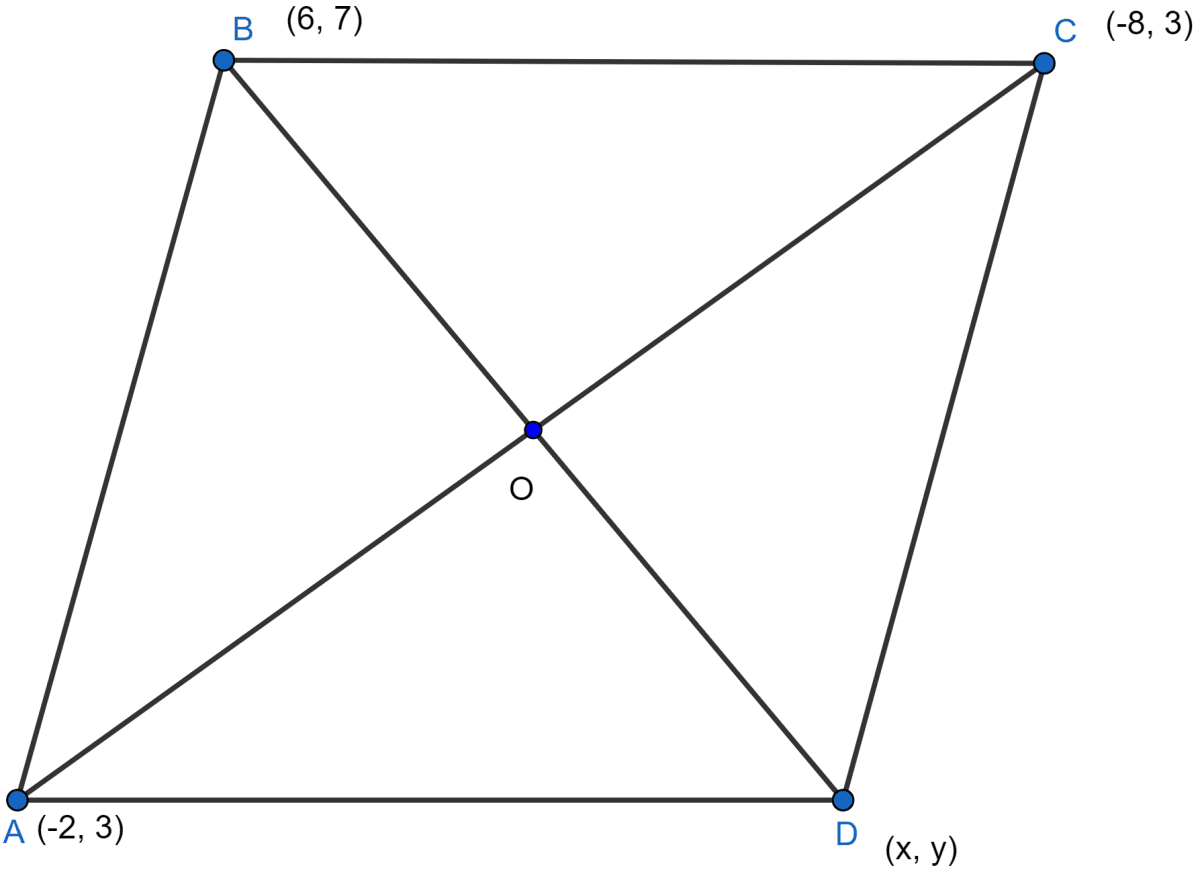
So, by mid-point formula the coordinates of O are,

$= \Big(\dfrac{-2 + 8}{2}, \dfrac{3 + 3}{2}\Big) \\[1em] = \Big(\dfrac{6}{2}, \dfrac{6}{2}\Big) \\[1em] = (3, 3).$

Since, (3, 3) is the mid-point of BD so,

$\Rightarrow 3 = \dfrac{x + 6}{2} \text{ and } 3 = \dfrac{y + 7}{2} \\[1em] \Rightarrow 6 = x + 6 \text{ and } 6 = y + 7 \\[1em] \Rightarrow x = 6 - 6 \text{ and } y = 6 - 7 \\[1em] \Rightarrow x = 0 \text{ and } y = -1.$

∴ Coordinates of D are (0, -1).

Hence, Option 2 is the correct option.