Mathematics
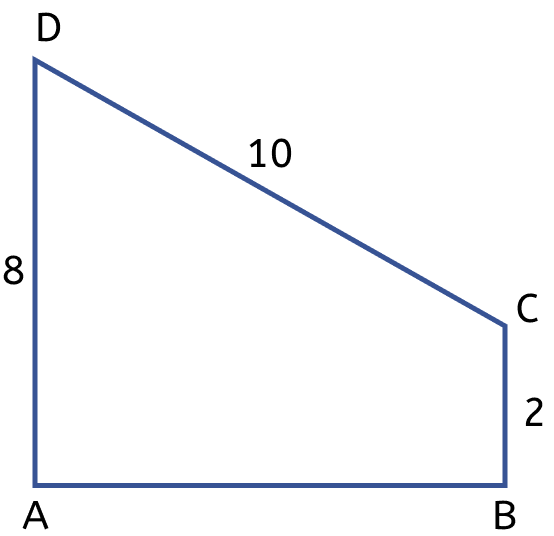
The figure (ii) given below is a trapezium. Find
(i) AB
(ii) area of trapezium ABCD.
Mensuration
21 Likes
Answer
(i) Construct a perpendicular from C to AD parallel to AB.
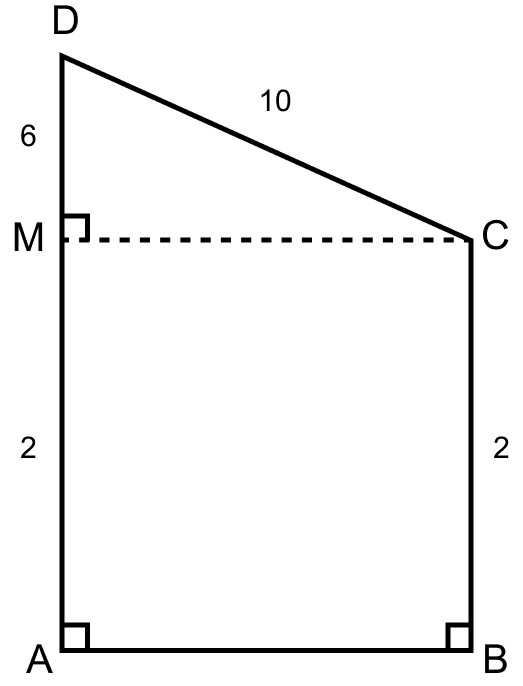
So, ABCM is a rectangle. Since, opposite sides of a rectangle are equal.
∴ AM = CB = 2 units.
From figure,
⇒ AD = AM + MD
⇒ MD = AD - AM = 8 - 2 = 6 units.
In right angle triangle MDC,
⇒ CD2 = MD2 + CM2
⇒ 102 = 62 + CM2
⇒ 100 = 36 + CM2
⇒ CM2 = 64
⇒ CM = = 8 units.
Since, ABCM is a rectangle.
∴ AB = CM = 8 units.
Hence, AB = 8 units.
(ii) Area of trapezium ABCD = × (sum of || sides) × distance between them
= × (AD + BC) × AB
= × (8 + 2) × 8
= 40 sq. units.
Hence, area of trapezium ABCD = 40 sq. units.
Answered By
10 Likes
Related Questions
If the sides of a rhombus are 5 cm each and one diagonal is 8 cm, calculate
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
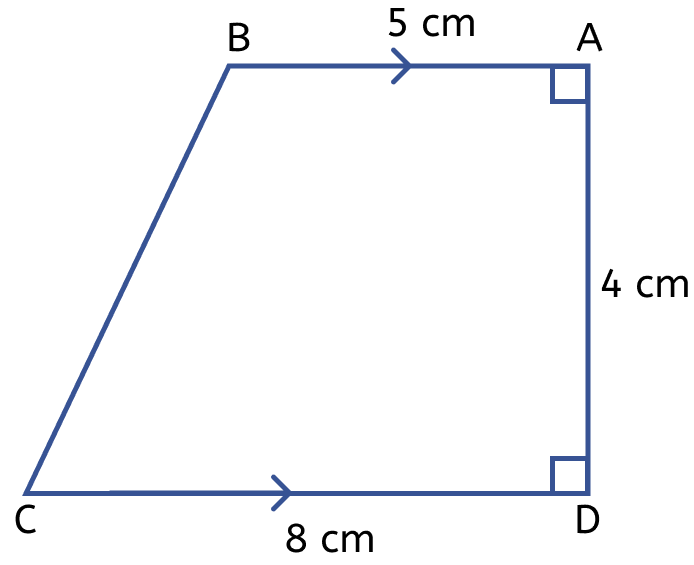
The figure (i) given below is a trapezium. Find the length of BC and the area of the trapezium. Assume AB = 5 cm, AD = 4 cm, CD = 8 cm.
The cross-section of a canal is shown in figure (iii) given below. If the canal is 8 m wide at the top and 6 m wide at the bottom and the area of the cross-section is 16.8 m2, calculate its depth.

The distance between parallel sides of a trapezium is 12 cm and the distance between mid-points of other sides is 18 cm. Find the area of the trapezium.