Mathematics
The figure (i) given below is a trapezium. Find the length of BC and the area of the trapezium. Assume AB = 5 cm, AD = 4 cm, CD = 8 cm.
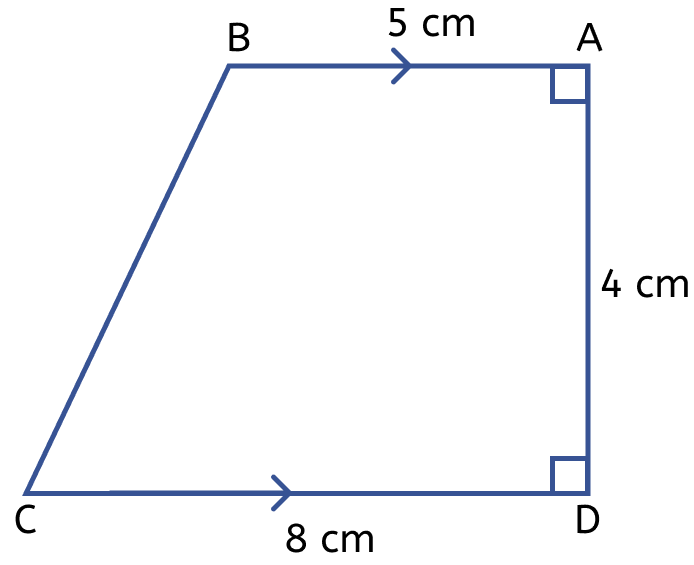
Mensuration
25 Likes
Answer
(a) Construct BN perpendicular to CD.
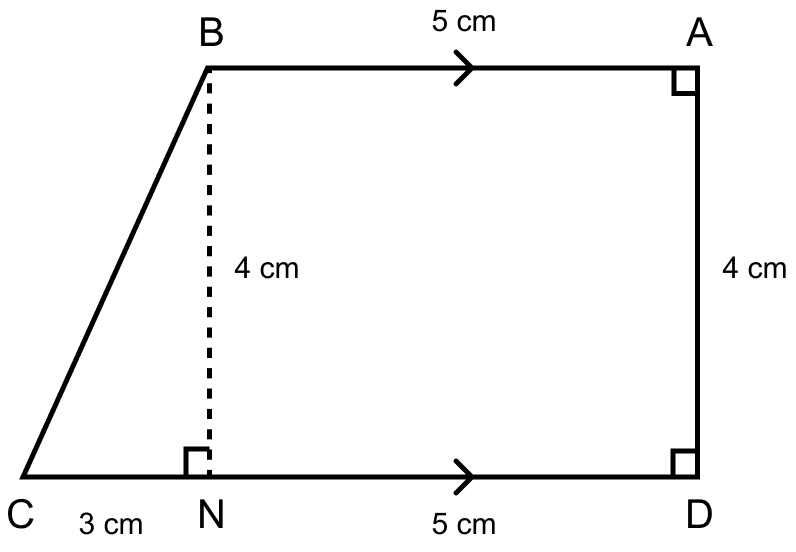
So, BADN is a rectangle.
As opposite sides of rectangle are equal.
∴ BN = AD = 4 cm and ND = BA = 5 cm.
From figure,
CN = CD – ND = 8 - 5 = 3 cm.
In right angle triangle BCN,
Using Pythagoras theorem,
⇒ BC2 = BN2 + CN2
⇒ BC2 = 42 + 32
⇒ BC2 = 16 + 9 = 25
⇒ BC = = 5 cm.
By formula,
Area of trapezium = × sum of parallel sides × height
= × (AB + CD) × AD
= × (5 + 8) × 4
= 13 × 2 = 26 cm2.
Hence, BC = 5 cm and area of trapezium = 26 cm2.
Answered By
12 Likes
Related Questions
If the diagonals of a rhombus are 8 cm and 6 cm, find its perimeter.
If the sides of a rhombus are 5 cm each and one diagonal is 8 cm, calculate
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
The figure (ii) given below is a trapezium. Find
(i) AB
(ii) area of trapezium ABCD.
The cross-section of a canal is shown in figure (iii) given below. If the canal is 8 m wide at the top and 6 m wide at the bottom and the area of the cross-section is 16.8 m2, calculate its depth.
