Mathematics
The figure (i) given below shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in cm and all angles in the figure are right angles.

Mensuration
26 Likes
Answer
(a) From figure,

The line AB divides the figure, into two cuboids vertical and horizontal.
Volume of solid = Volume of vertical cuboid + Volume of horizontal cuboid
= 4 × 2 × 6 + 4 × 4 × 2
= 48 + 32
= 80 cm3
Hence, volume of solid = 80 cm3.
Answered By
16 Likes
Related Questions
Three cubes whose edges are x cm, 8 cm and 10 cm respectively are melted and recast into a single cube of edge 12 cm. Find x.
The area of cross-section of a pipe is 3.5 cm2 and water is flowing out of pipe at the rate of 40 cm/s. How much water is delivered by the pipe in one minute?
The figure (ii) given below shows the cross section of a concrete wall to be constructed. It is 2 m wide at the top, 3.5 m wide at the bottom and its height is 6 m and its length is 400 m. Calculate
(i) the cross sectional area and
(ii) volume of concrete in the wall.

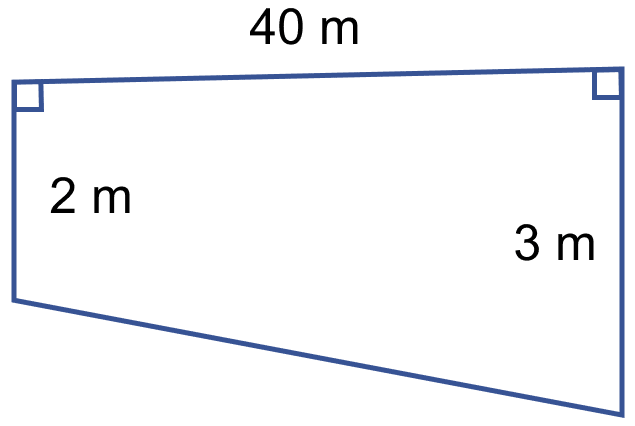
The figure (iii) given below show the cross-section of a swimming pool 10 m broad, 2 m deep at one end and 3 m deep at the other end. Calculate the volume of water it will hold when full, given that its length is 40 m.