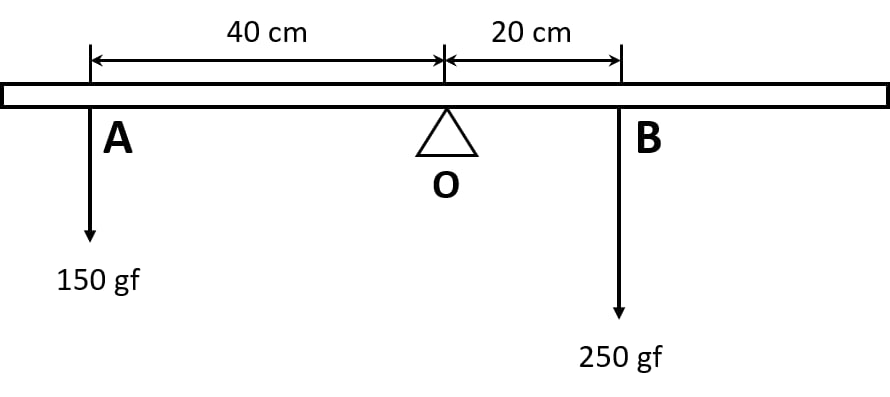
The diagram shows a uniform meter rule weighing 100 gf, pivoted at its centre O. Two weights 150gf and 250gf hang from the point A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm.

Calculate:

(i) the total anticlockwise moment about O,

(ii) the total clockwise moment about O,

(iii) the difference of anticlockwise and clockwise moment, and

(iv) the distance from O where a 100gf weight should be placed to balance the metre rule.

(i) The total anticlockwise moment about the centre o

$= 150gf \times 40cm \ = 6000gf cm$

The total clockwise moment about the centre o

$= 250gf \times 20cm \\[0.5em] = 5000gf cm \\[0.5em]$

(iii) The difference of anticlockwise and clockwise moment

$= 6000 - 5000 \\[0.5em] = 1000gf cm \\[0.5em]$

(iv) As we know, the principle of moments states that

Anticlockwise moment = Clockwise moment

$150gf \times 40cm = 250gf \times 20cm + 100gf \times d \\[0.5em] 6000gf = 5000gf +100gf \times d \\[0.5em] d = \dfrac {1000}{100} \\[0.5em] d = 10cm$

So d = 10 cm on the right side of o