Physics
A uniform half metre rule can be balanced at the 29.0 cm mark when a mass 20g is hung from its one end.
(a) Draw a diagram of the arrangement.
(b) Find the mass of the half metre rule.
(c) In which direction would the balancing point shift if 20g mass is shifted inside from its one end?
Force
439 Likes
Answer
(a) Diagram of the arrangement is shown below:

(b) Suppose, if the mass of the metre rule be M.
Given, uniform metre rule, so weight (Mg) will act at 25 cm.
Mg produces anticlockwise moment about point o.
Now, in order to balance the 20g weight is tied at 50cm point and it acts in the clockwise direction.
As we know, the principle of moments states that
Anticlockwise moment = Clockwise moment
The weight of half the metre rule is 105 g.
(c) The balancing point will shift towards the 25 cm mark.
Answered By
279 Likes
Related Questions
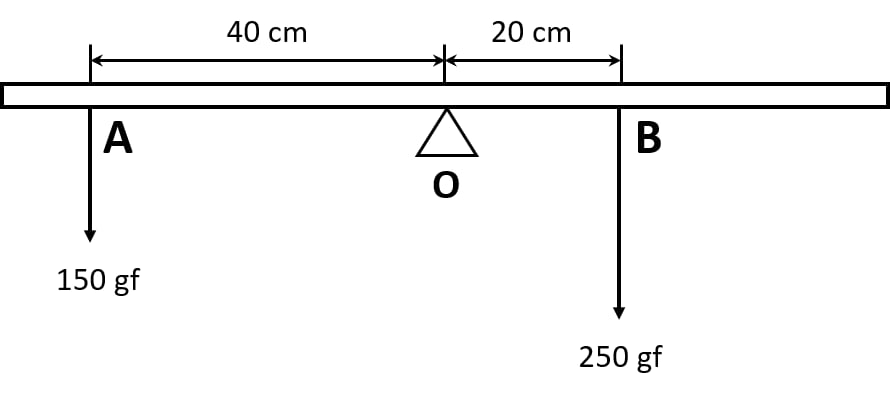
The diagram shows a uniform meter rule weighing 100 gf, pivoted at its centre O. Two weights 150gf and 250gf hang from the point A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm.
Calculate:
(i) the total anticlockwise moment about O,
(ii) the total clockwise moment about O,
(iii) the difference of anticlockwise and clockwise moment, and
(iv) the distance from O where a 100gf weight should be placed to balance the metre rule.
A uniform metre rule of weight 10 gf is pivoted at its 0 mark.
(i) What moment of force depresses the rule?
(ii) How can it be made horizontal by applying a least force?
A uniform metre rule of mass 100 g is balanced on a fulcrum at mark 40 cm by suspending an unknown mass m at the mark 20 cm.
(i) Find the value of m.
(ii) To which side the rule will tilt if the mass m is moved to the mark 10 cm?
(iii) What is the resultant moment now?
(iv) How can it be balanced by another mass 50 g?
In figure below, a uniform bar of length l m is supported at its ends and loaded by a weight W kgf at its middle. In equilibrium, find the reactions R1 and R2 at the ends.
