Mathematics
The daily wages of 80 workers in a project are given below :
| Wages (in ₹) | No. of workers |
|---|---|
| 400 - 450 | 2 |
| 450 - 500 | 6 |
| 500 - 550 | 12 |
| 550 - 600 | 18 |
| 600 - 650 | 24 |
| 650 - 700 | 13 |
| 700 - 750 | 5 |
Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = ₹ 50 on x-axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate :
(i) the median wage of the workers.
(ii) the lower quartile wage of the workers.
(iii) the number of workers who earn more than ₹625 daily.
Measures of Central Tendency
15 Likes
Answer
- The cumulative frequency table for the given continuous distribution is :
| Wages (in ₹) | No. of workers | Cumulative frequency |
|---|---|---|
| 400 - 450 | 2 | 2 |
| 450 - 500 | 6 | 8 |
| 500 - 550 | 12 | 20 |
| 550 - 600 | 18 | 38 |
| 600 - 650 | 24 | 62 |
| 650 - 700 | 13 | 75 |
| 700 - 750 | 5 | 80 |
Take 2 cm along x-axis = 50 rupees
Take 1 cm along y-axis = 10 workers
Since, scale on x-axis starts at 400, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 400.
Plot the points (450, 2), (500, 8), (550, 20), (600, 38), (650, 62), (700, 75) and (750, 80) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 400 - 450.Join these points by a freehand drawing.
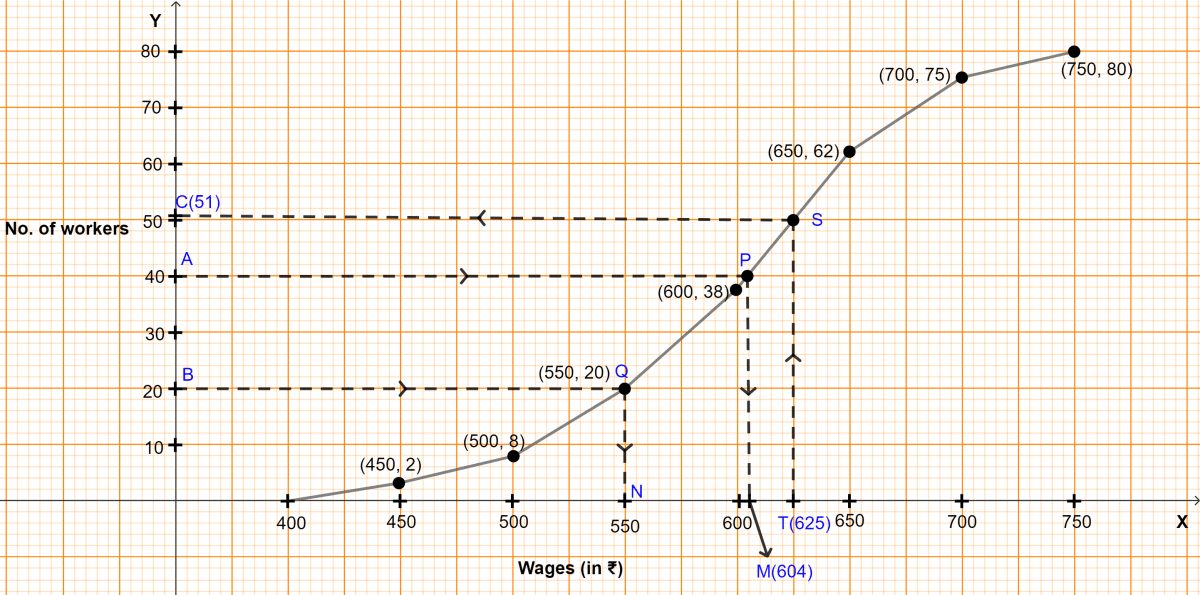
The required ogive is shown in figure above.
(i) Here, n (no. of students) = 80.
To find the median :
Let A be the point on y-axis representing frequency = = 40.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 604.
Hence, the required median wage = ₹604.
(ii) To find lower quartile :
Let B be the point on y-axis representing frequency = = 20
Through B, draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 550.
Hence, lower quartile wage = ₹550.
(iii) Let T be the point on x-axis representing wage = ₹625.
Through T, draw a vertical line to meet the ogive at S. Through S, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 51.
Workers who earn less than ₹625 = 51.
So, workers earning more than ₹625 = Total workers - workers who earn less than ₹625 = 80 - 51 = 29.
Hence, there are 29 workers earning more more than ₹625 daily.
Answered By
7 Likes
Related Questions
The weight of 50 workers is given below :
Weight (in kg) No. of workers 50 - 60 4 60 - 70 7 70 - 80 11 80 - 90 14 90 - 100 6 100 - 110 5 110 - 120 3 Draw an ogive of the given distribution using a graph sheet. Take 2 cm = 10 kg on one axis and 2 cm = 5 workers along the other axis. Use a graph to estimate the following :
(i) the upper and lower quartiles.
(ii) if weighing 95 kg and above is considered overweight find the number of workers who are overweight.
Marks obtained by 200 students in an examination are given below :
Marks No. of students 0 - 10 5 10 - 20 11 20 - 30 10 30 - 40 20 40 - 50 28 50 - 60 37 60 - 70 40 70 - 80 29 80 - 90 14 90 - 100 6 Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) The median marks
(ii) The number of students who failed if minimum marks required to pass is 40.
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.
The table shows the distribution of scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution.
(Take 2 cm = 10 scores on the x-axis and 2 cm = 20 shooters on the y-axis)
Scores No. of shooters 0 - 10 9 10 - 20 13 20 - 30 20 30 - 40 26 40 - 50 30 50 - 60 22 60 - 70 15 70 - 80 10 80 - 90 8 90 - 100 7 Use your graph to estimate the following :
(i) The median.
(ii) The inter quartile range.
(iii) The number of shooters who obtained a score of more than 85%.
The monthly income of a group of 320 employees in a company is given below :
Monthly Income (in ₹) No. of Employees 6000 - 7000 20 7000 - 8000 45 8000 - 9000 65 9000 - 10000 95 10000 - 11000 60 11000 - 12000 30 12000 - 13000 5 Draw an ogive of the given distribution on a graph sheet taking 2 cm = ₹1000 on one axis and 2 cm = 50 employees on the other axis. From the graph, determine :
(i) The median wage.
(ii) The number of employees whose income is below ₹8500.
(iii) If the salary of a senior employee is above ₹11500, find the number of senior employees in the company.
(iv) The upper quartile.