Mathematics
The monthly income of a group of 320 employees in a company is given below :
| Monthly Income (in ₹) | No. of Employees |
|---|---|
| 6000 - 7000 | 20 |
| 7000 - 8000 | 45 |
| 8000 - 9000 | 65 |
| 9000 - 10000 | 95 |
| 10000 - 11000 | 60 |
| 11000 - 12000 | 30 |
| 12000 - 13000 | 5 |
Draw an ogive of the given distribution on a graph sheet taking 2 cm = ₹1000 on one axis and 2 cm = 50 employees on the other axis. From the graph, determine :
(i) The median wage.
(ii) The number of employees whose income is below ₹8500.
(iii) If the salary of a senior employee is above ₹11500, find the number of senior employees in the company.
(iv) The upper quartile.
Measures of Central Tendency
23 Likes
Answer
- The cumulative frequency table for the given continuous distribution is :
| Monthly Income (in ₹) | No. of Employees | Cumulative frequency |
|---|---|---|
| 6000 - 7000 | 20 | 20 |
| 7000 - 8000 | 45 | 65 |
| 8000 - 9000 | 65 | 130 |
| 9000 - 10000 | 95 | 225 |
| 10000 - 11000 | 60 | 285 |
| 11000 - 12000 | 30 | 315 |
| 12000 - 13000 | 5 | 320 |
Take 2 cm along x-axis = 1000 (₹)
Take 1 cm along y-axis = 50 (Employees)
Since, scale on x-axis starts at 6000, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 6000.
Plot the points (7000, 20), (8000, 65), (9000, 130), (10000, 225), (11000, 285), (12000, 315) and (13000, 320) representing upper class limits and the respective cumulative frequencies.
Also plot the point representing lower limit of the first class i.e. 6000 - 7000.Join these points by a freehand drawing.
The required ogive is shown in figure above.
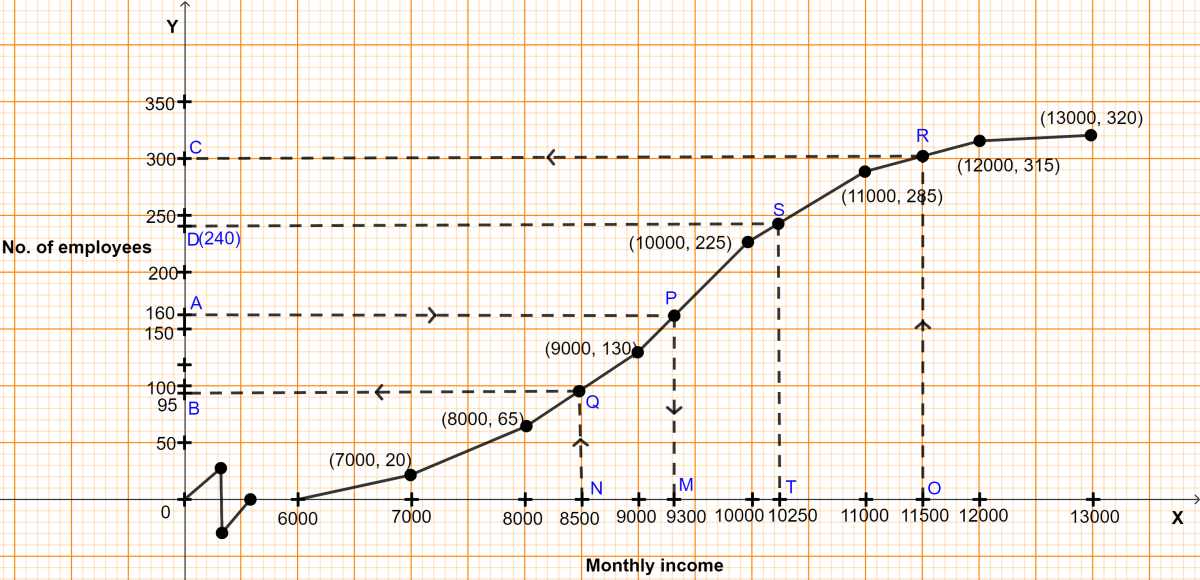
(i) Here, n (no. of students) = 320.
To find the median :
Let A be the point on y-axis representing frequency = = 160.
Through A draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 9300.
Hence, the required median income = ₹9300.
(ii) Let N be the point on x-axis representing income = ₹8500.
Through N, draw a vertical line to meet the ogive at Q. Through Q, draw a horizontal line to meet the y-axis at B. The ordinate of the point B represents 95.
Hence, no. of employees earning less than ₹8500 = 95.
(iii) Let O be the point on x-axis representing income = ₹11500.
Through O, draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 300.
No. of employees earning less than ₹11500 = 300
So, no. of employees earning more than ₹11500 = Total employees - employees earning less than ₹11500 = 320 - 300 = 20.
Hence, there are 20 senior employees in the company.
(iv) To find upper quartile :
Let D be the point on y-axis representing frequency = = 240.
Through D, draw a horizontal line to meet the ogive at S. Through S, draw a vertical line to meet the x-axis at T. The abscissa of the point T represents ₹10250.
Hence, upper quartile = ₹10250.
Answered By
3 Likes
Related Questions
The daily wages of 80 workers in a project are given below :
Wages (in ₹) No. of workers 400 - 450 2 450 - 500 6 500 - 550 12 550 - 600 18 600 - 650 24 650 - 700 13 700 - 750 5 Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = ₹ 50 on x-axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate :
(i) the median wage of the workers.
(ii) the lower quartile wage of the workers.
(iii) the number of workers who earn more than ₹625 daily.
Use graph paper for this question.
A survey regarding height (in cm) of 60 boys belonging to class 10 of a school was conducted. The following data was recorded :
Height (in cm) No. of boys 135 - 140 4 140 - 145 8 145 - 150 20 150 - 155 14 155 - 160 7 160 - 165 6 165 - 170 1 Taking 2 cm = height of 10 cm on one axis and 2 cm = 10 boys along the other axis, draw an ogive of the above distribution. Use the graph to estimate the following :
(i) median
(ii) lower quartile
(iii) if above 158 is considered as the tall boy of the class, find the number of boys in the class who are tall.
Marks obtained by 200 students in an examination are given below :
Marks No. of students 0 - 10 5 10 - 20 11 20 - 30 10 30 - 40 20 40 - 50 28 50 - 60 37 60 - 70 40 70 - 80 29 80 - 90 14 90 - 100 6 Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) The median marks
(ii) The number of students who failed if minimum marks required to pass is 40.
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.
The marks obtained by 100 students in a Mathematics test are given below :
Marks No. of students 0 - 10 3 10 - 20 7 20 - 30 12 30 - 40 17 40 - 50 23 50 - 60 14 60 - 70 9 70 - 80 6 80 - 90 5 90 - 100 4 Draw an ogive on a graph sheet and from it determine the :
(i) median
(ii) lower quartile
(iii) number of students who obtained more than 85% marks in the test
(iv) number of students who did not pass in the test if the pass percentage was 35.