Mathematics
The adjoining figure shows an equilateral triangle OAB with each side = 2a units. Find the coordinates of the vertices.
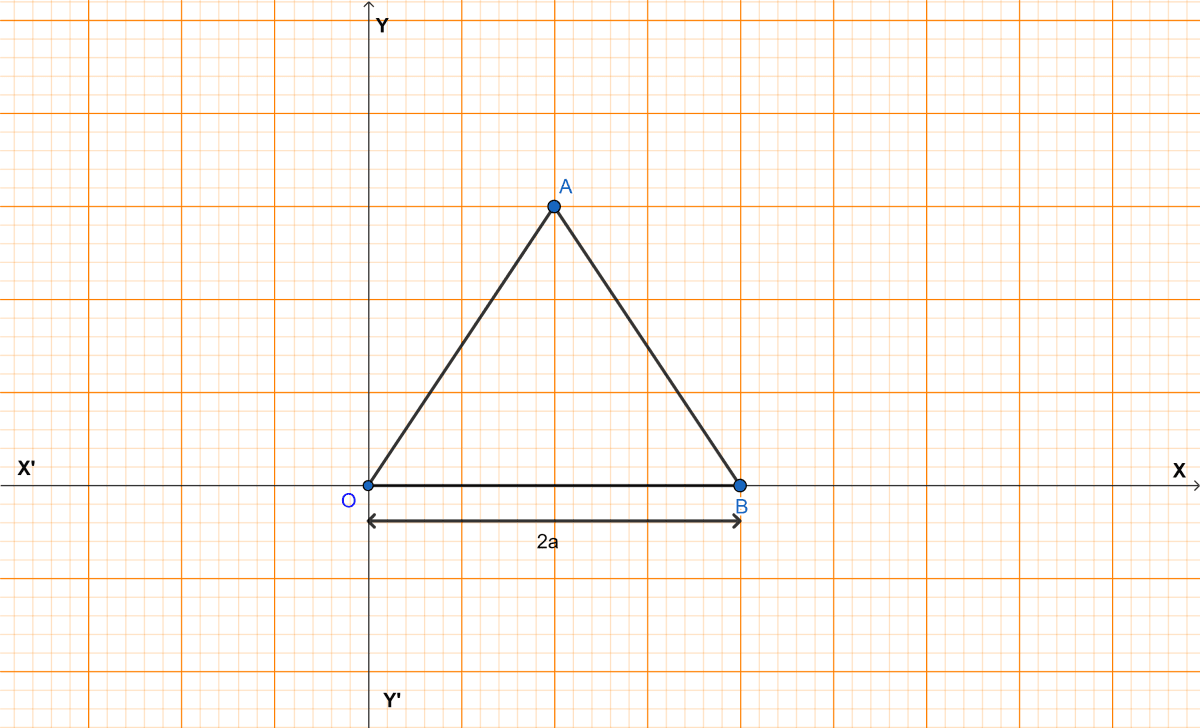
Coordinate Geometry
36 Likes
Answer
Given equilateral triangle OAB.
OA = OB = AB = 2a units.
Draw AD ⊥ OB.
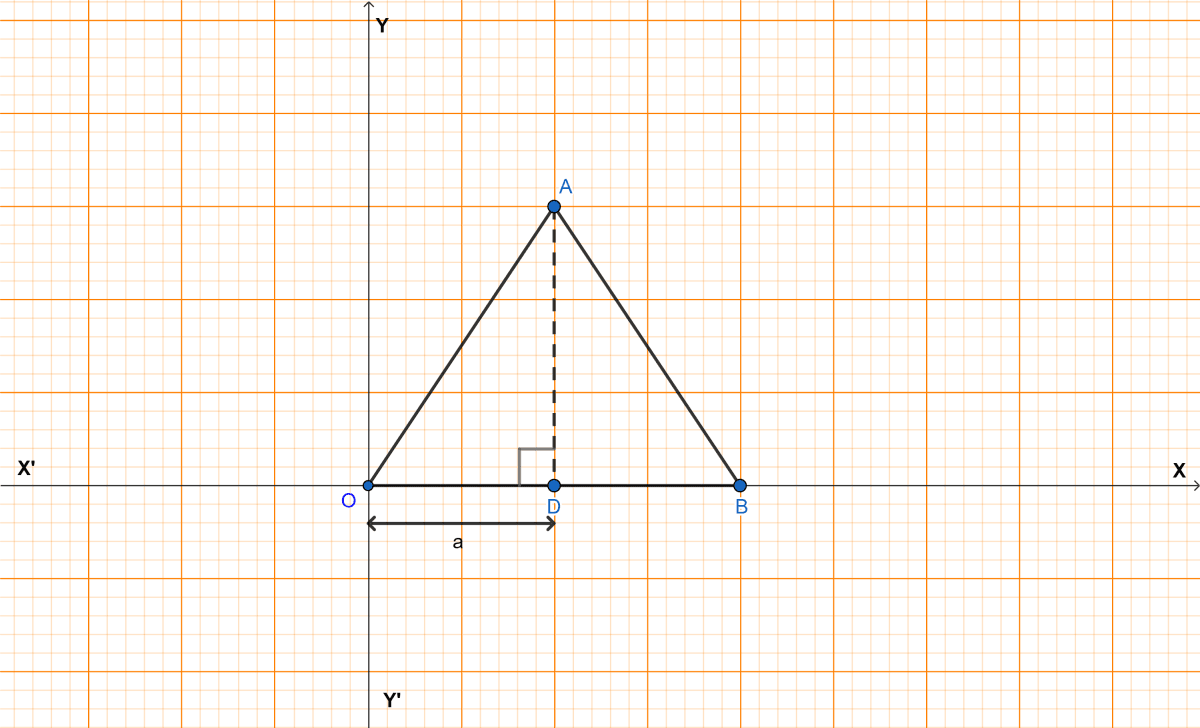
In an equilateral triangle, a perpendicular drawn from one of the vertices to the opposite side bisects the side.
∴ OD = x OB = x 2a = a.
In right angle triangle OAD,
⇒ OA2 = OD2 + AD2
⇒ (2a)2 = a2 + AD2
⇒ 4a2 = a2 + AD2
⇒ AD2 = 4a2 - a2
⇒ AD2 = 3a2
⇒ AD = units.
⇒ AD = a units.
From graph,
Co-ordinates of O = (0, 0)
Co-ordinates of B = (2a, 0)
As, OD = a units and AD = a units.
Co-ordinates of A = (a, a).
Hence, co-ordinates of O = (0, 0), B = (2a, 0) and A = (a, a).
Answered By
21 Likes
Related Questions
Write the co-ordinates of the vertices of a rectangle which is 6 units long and 4 units wide if the rectangle is in the first quadrant, its longer side lies on the x-axis and one vertex is at the origin.
In the adjoining figure, ABCD is a rectangle with length 6 units and breadth 3 units. If O is the mid-point of AB, find the coordinates of A, B, C and D.

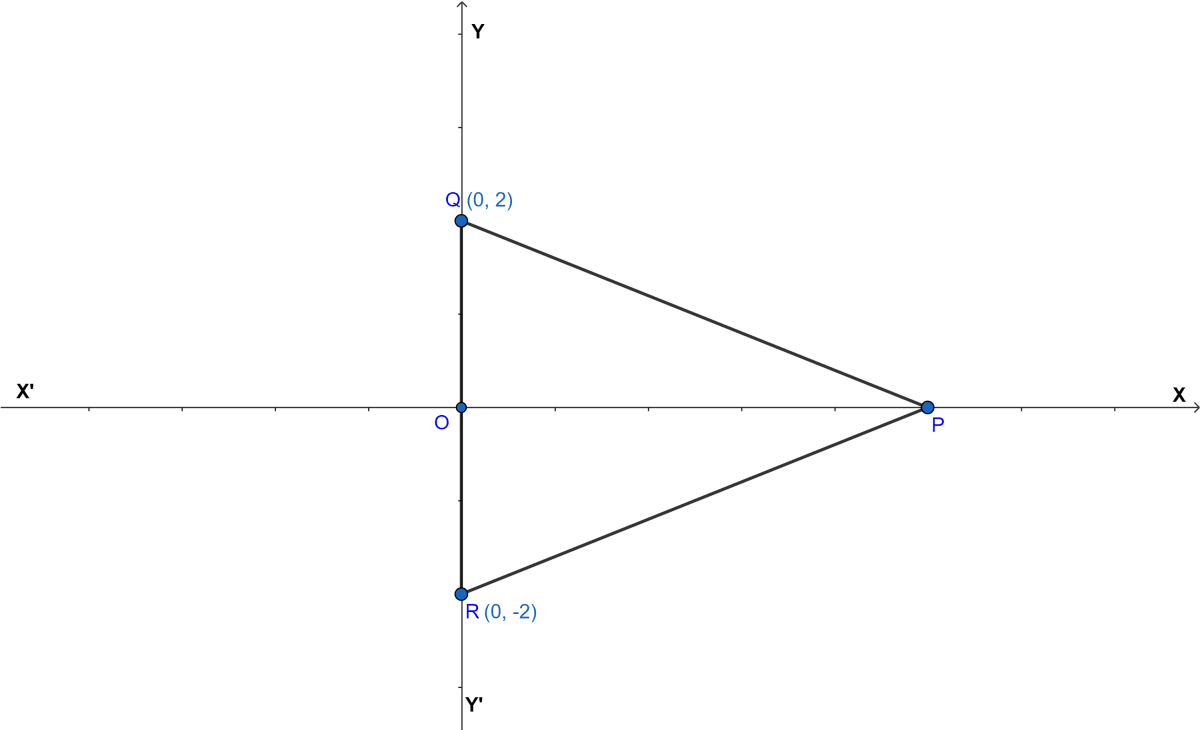
In the given figure, △PQR is equilateral. If the coordinates of the points Q and R are (0, 2) and (0, -2) respectively, find the coordinates of the point P.
Draw the graph of the following linear equation :
2x + y + 3 = 0