Mathematics
Take 1 cm to represent 1 unit on each axis to draw the graphs of the equations 4x - 5y = -4 and 3x = 2y - 3 on the same graph sheet (same axes). Use your graph to find the solution of the above simultaneous equations.
Coordinate Geometry
29 Likes
Answer
Given,
Equation :
⇒ 4x - 5y = -4
⇒ 5y = 4x + 4
⇒ y = ………….(1)
When, x = -1, y = = 0,
x = 1.5, y = = 2,
x = 4, y = = 4.
Table of values for equation (1)
| x | -1 | 1.5 | 4 |
|---|---|---|---|
| y | 0 | 2 | 4 |
Steps of construction :
Plot the points (-1, 0), (1.5, 2) and (4, 4) on graph paper.
Connect points by straight line.
Given,
Equation :
⇒ 3x = 2y - 3
⇒ 2y = 3x + 3
⇒ y = …………(2)
When, x = -1, y = = 0,
x = 0, = 1.5,
x = 1, = 3.
Table of values for equation (2)
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0 | 1.5 | 3 |
Steps of construction :
Plot the points (-1, 0), (0, 1.5) and (1, 3) on graph paper.
Connect points by straight line.
The graphs of both the straight lines are shown in the figure.
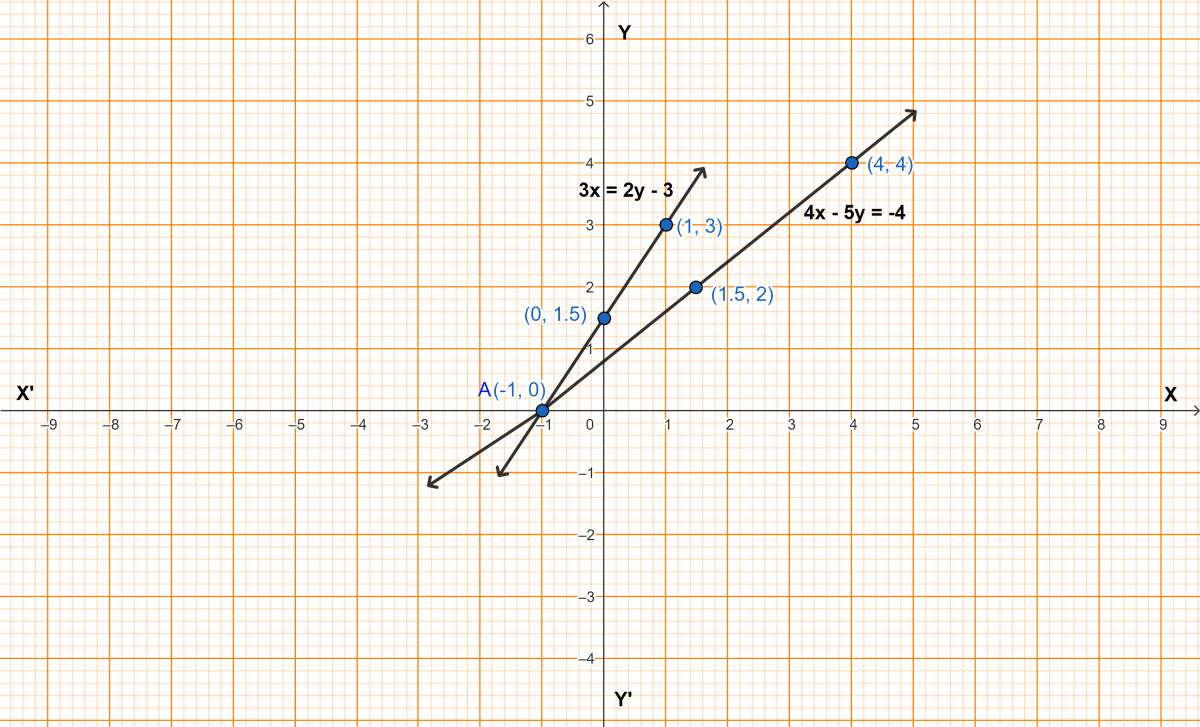
The lines intersect at point A(-1, 0).
Hence, the solution of the given equations is x = -1, y = 0.
Answered By
8 Likes
Related Questions
Solve the following pair of equations graphically. Plot atleast 3 points for each straight line.
2x - 7y = 6, 5x - 8y = -4.
Using the same axes of coordinates and the same unit, solve graphically.
x + y = 0, 3x - 2y = 10.
Solve the following simultaneous equations graphically :
x + 3y = 8, 3x = 2 + 2y.
Solve graphically the simultaneous equations 3y = 5 - x, 2x = y + 3.