Mathematics
Spherical marbles of diameter 1.4 cm are dropped into a beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it if the water rises by 5.6 cm?
Mensuration
6 Likes
Answer
Given,
Diameter of spherical marbles = 1.4 cm
Radius (r) = = 0.7 cm.
Diameter of beaker = 7 cm
Radius of beaker (R) = = 3.5 cm
Increase in water level (h) = 5.6 cm.
Let n marbles are dropped.
⇒ Volume of water increased in beaker = n × Volume of one marble (sphere)
⇒ πR2h =
Hence, 150 marbles are dropped in the beaker.
Answered By
4 Likes
Related Questions
A circus tent is cylindrical to a height of 8 m surmounted by a conical part. If total height of the tent is 13 m and the diameter of its base is 24 m; calculate:
(i) total surface area of the tent
(ii) area of canvas, required to make this tent allowing 10% of the canvas used for folds and stitching.
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm × 14 cm × 10.5 cm. Find the rise in level of the water when the solid is submerged.
The given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic meters correct to one place of decimal.
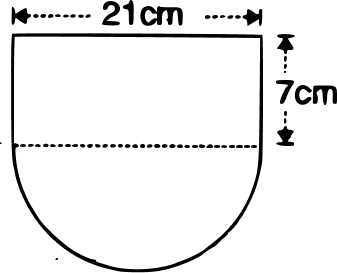
An open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is cm and the radius of whose base is 2 cm, find the drop in the water level.