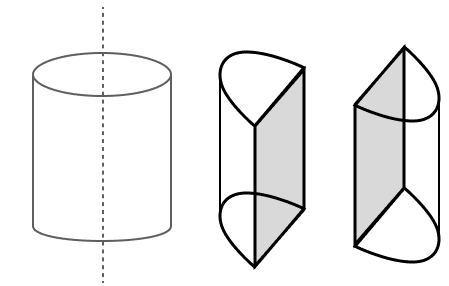
A solid metallic cylinder is cut into two identical halves along its height. The diameter of the cylinder is 7 cm and the height is 10 cm. Find :

(a) The total surface area (both the halves).

(b) The total cost of painting the two halves at the rate of ₹ 30 per cm².

$\Big(\text{use } \pi = \dfrac{22}{7}\Big)$

(a) Given,

Diameter of cylinder (d) = 7 cm

Radius of cylinder (r) = $\dfrac{d}{2} = \dfrac{7}{2}$ = 3.5 cm

Height of cylinder (h) = 10 cm

Total surface area (both the halves) = Total surface area of cylinder + Area of two rectangles

= [2πr(h + r)] + [2 × (l × b)]

= [2πr(h + r)] + [2 × (h × d)]

= $\Big[2 \times \dfrac{22}{7} \times 3.5 \times (3.5 + 10) \Big] + [2 \times 10 \times 7]$

= (2 × 22 × 0.5 × 13.5) + 140

= 297 + 140

= 437 cm².

Hence, total surface area of both the halves = 437 cm².

(b) Total cost of painting the two halves = Total surface area × Rate

= 437 × 30

= ₹ 13,110.

Hence, total cost of painting the two halves = ₹ 13,110.