Show that the sum of kinetic energy and potential energy (i.e., total mechanical energy) is always conserved in the case of a freely falling body under gravity (with air resistance neglected) from a height h by finding it when

(i) the body is at the top,

(ii) the body has fallen a distance x,

(iii) the body has reached the ground.

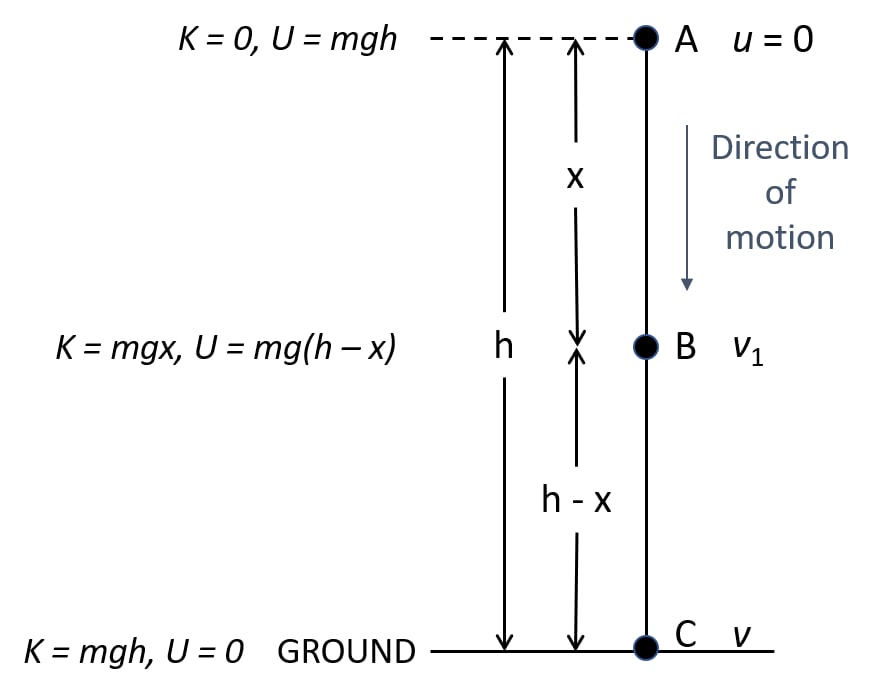
We know that,

Kinetic energy + potential energy = constant

So, when a body falls from a height h under free fall

(i) At the position A — height h

Initial velocity = 0

Kinetic energy K = 0

Potential energy U = mgh

As, Total energy = KE + PE

Total energy = 0 + mgh

Total energy = mgh       (1)

(ii) At the position B — when it has fallen a distance x.

Then, velocity at B = v₁

Then u = 0, s = x, a = g

From equation of motion:
v² = u² + 2aS
v₁² = 0 + 2gx = 2gx

$\therefore \text{Kinetic energy K}= \dfrac{1}{2} \times m \times v_1^2 \\[0.5em] = \dfrac{1}{2} \times m \times 2gx \\[0.5em] = mgx$

∴ Potential energy U = mg (h – x)

Hence, total energy = K + U = mgx + mg (h – x) = mgh

Total energy = mgh       (2)

(iii) At position C (on the ground) —

Let the velocity acquired by the body on reaching the ground be v₂.

Then u = 0, s = h, a = g

We know,
v²= u² + 2aS
v₂² = 0 + 2gh
v₂² = 2gh

$\therefore \text{Kinetic energy K}= \dfrac{1}{2} \times m \times v_2^2 \\[0.5em] = \dfrac{1}{2} \times m \times 2gh \\[0.5em] = mgh$

And potential energy U = 0 (at the ground when h = 0)

So, total energy = K + U = mgh + 0

Total energy = mgh       (3)

Thus, from equation (1), (2) and (3) we note that the total mechanical energy i.e. the sum of kinetic energy and potential energy always remain constant at each point of motion and it is equal to the initial potential energy at height h.