Mathematics
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.
Mid-point Theorem
26 Likes
Answer
Let ABCD be a square in which E, F, G and H are midpoints of AB, BC, CD and DA respectively.
Join EF, FG, GH and HE.
Join AC and BD.
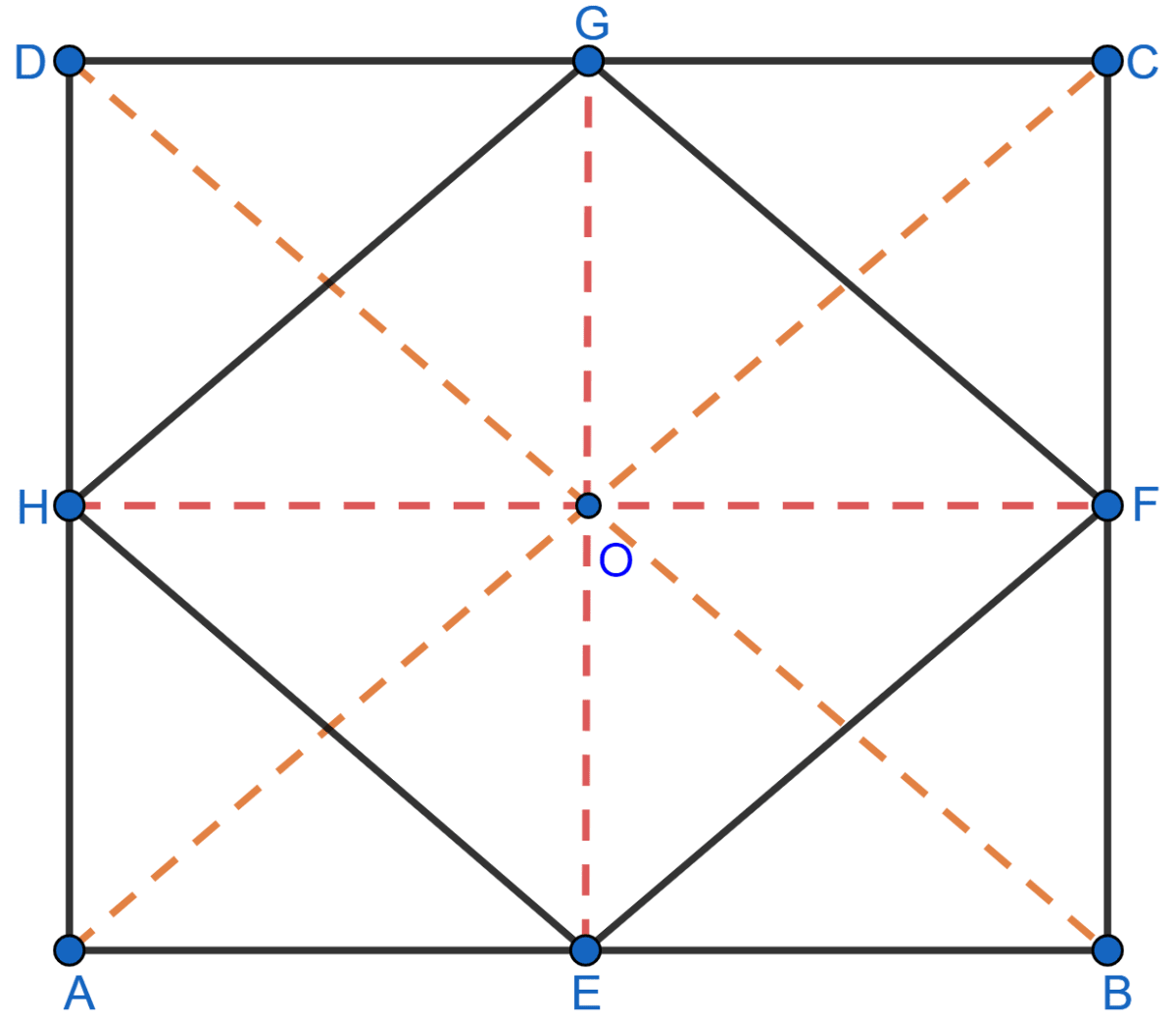
In △ACD,
G and H are mid-points of CD and AD respectively,
∴ GH || AC and GH = AC …….(i)
In △ABC,
E and F are mid-points of AB and BC respectively,
∴ EF || AC and EF = AC …….(ii)
Using (i) and (ii) we get,
EF || GH and EF = GH = AC ……..(1)
In △ABD,
E and H are mid-points of AB and AD respectively,
∴ EH || BD and EH = BD …….(iii)
In △BCD,
G and F are mid-points of CD and BC respectively,
∴ FG || BD and FG = BD …….(iv)
Using (iii) and (iv) we get,
EH || FG and EH = FG = BD ……..(2)
We know that diagonals of square are equal,
AC = BD
Dividing both sides by 2 we get,
Substituting above value in 1 and 2 we get,
EF = GH = EH = FG ………(v)
∴ EFGH is a parallelogram.
In △GOH and △GOF,
OH = OF as diagonals of parallelogram bisect each other.
OG = OG (Common)
GH = GF (From (v))
∴ △GOH ≅ △GOF (SSS axiom of congruency)
∠GOH = ∠GOF (c.p.c.t.c.)
From figure,
⇒ ∠GOH + ∠GOF = 180°
⇒ ∠GOH + ∠GOH = 180°
⇒ 2∠GOH = 180°
⇒ ∠GOH = 90°.
So, the diagonals of EFGH bisect and are perpendicular to each other.
∴ EFGH is a square.
Hence, proved that quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.
Answered By
20 Likes
Related Questions
The diagonals AC and BD of a parallelogram ABCD intersect at O. If P is the mid-point of AD, prove that
(i) PO || AB
(ii) PO = CD.
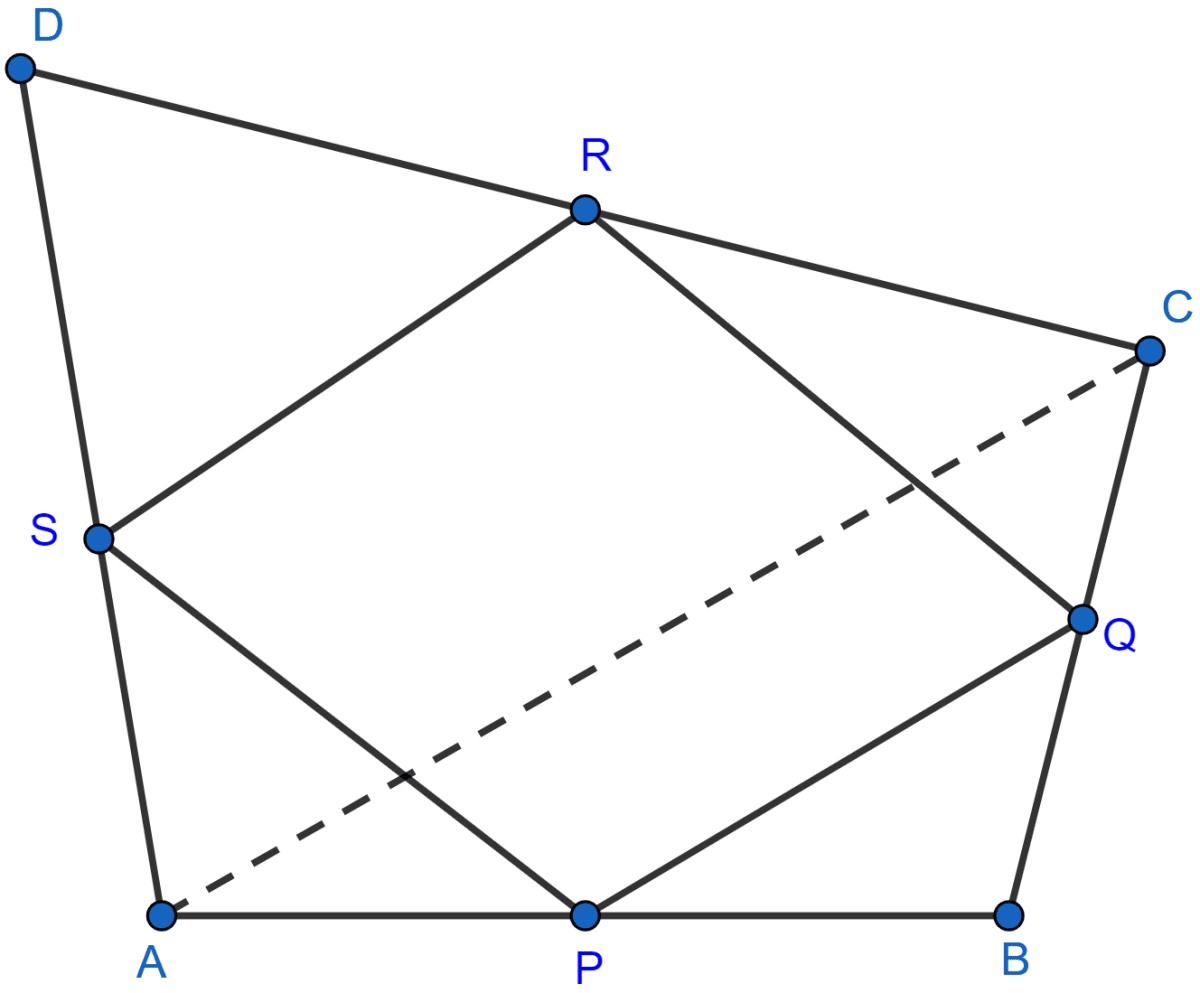
In the adjoining figure, ABCD is a quadrilateral in which P, Q, R and S are midpoints of AB, BC, CD and DA respectively. AC is its diagonal. Show that
(i) SR || AC and SR = AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
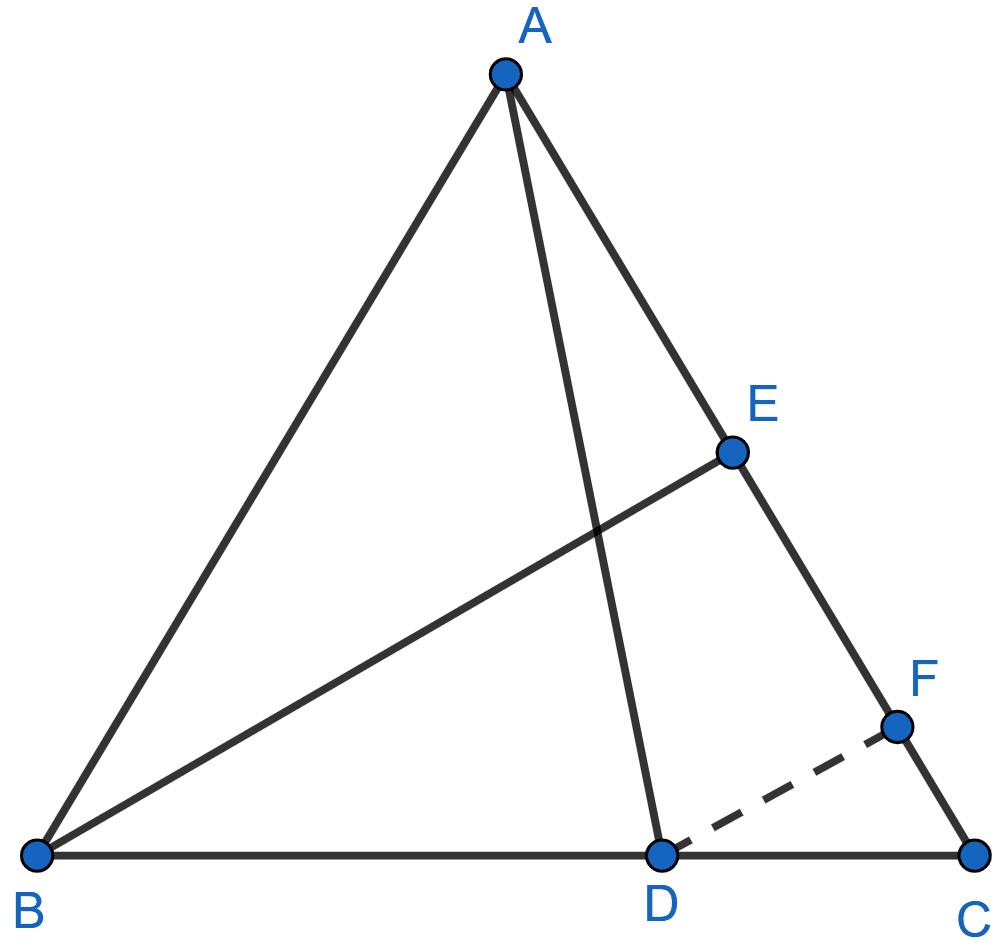
In the adjoining figure, AD and BE are medians of △ABC. If DF || BE, prove that CF =
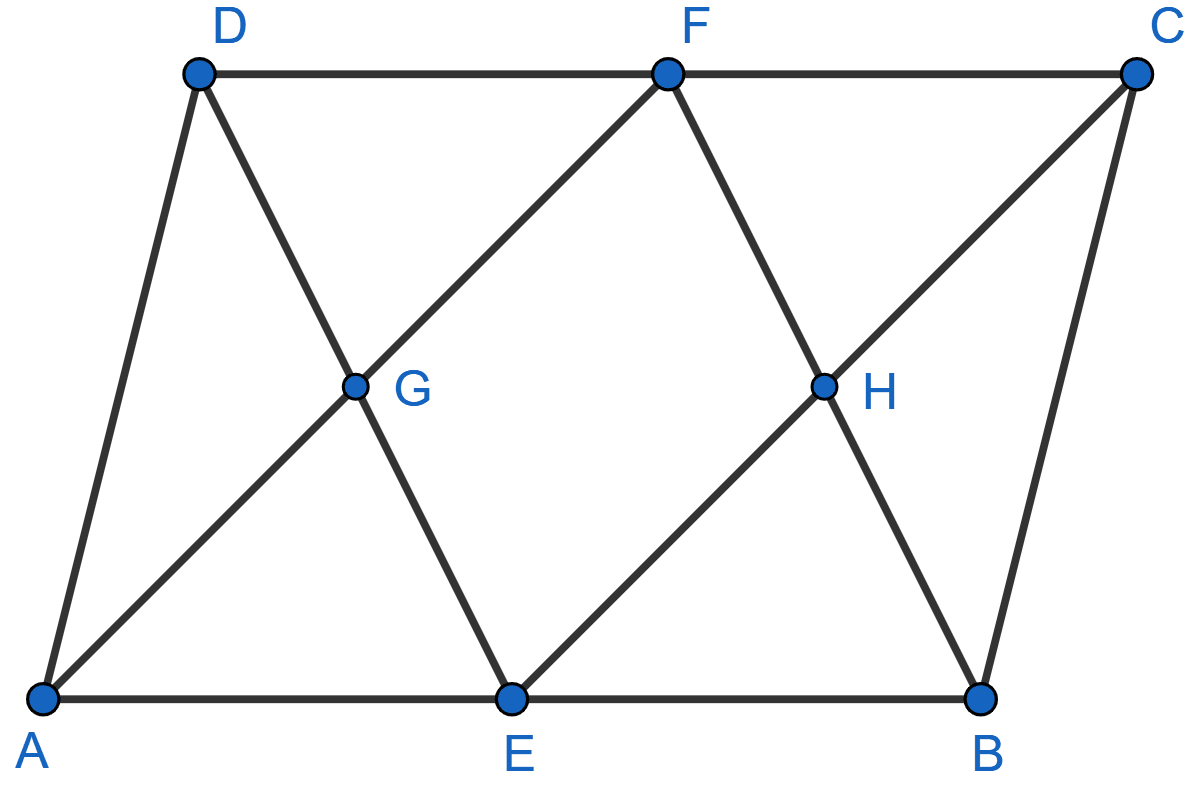
In the adjoining figure, ABCD is a parallelogram. E and F are mid-points of the sides AB and CD respectively. The straight lines AF and BF meet the straight lines ED and EC in points G and H respectively. Prove that
(i) △HEB ≅ △HCF
(ii) GEHF is a parallelogram.