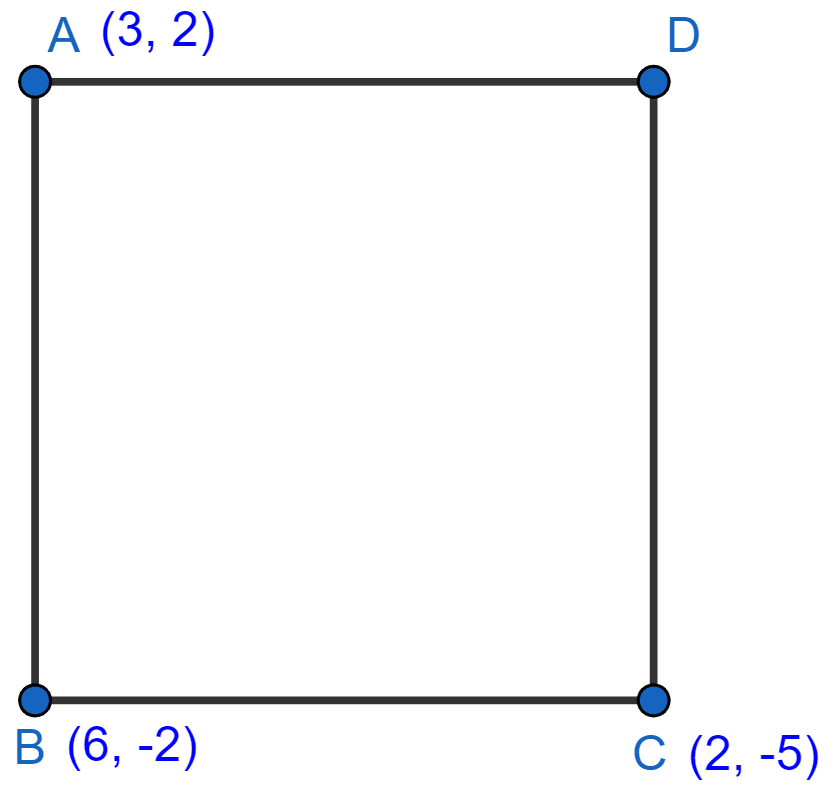
Show that A (3, 2), B (6, -2) and C (2, -5) can be the vertices of a square.

(i) Find the co-ordinates of its fourth vertex D, if ABCD is a square.

(ii) Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.

Given, A (3, 2), B (6, -2) and C (2, -5)

By distance formula,

Distance between two points = $\sqrt{(x$2 - x1)^2 + (y2 - y1)^2}

$\text{AB} = \sqrt{(6 - 3)^2 + (-2 - 2)^2} \\[1em] = \sqrt{(3)^2 + (-4)^2} \\[1em] = \sqrt{9 + 16} \\[1em] = \sqrt{25} \\[1em] = 5 \\[1.5em] \text{BC} = \sqrt{(2 - 6)^2 + (-5 - (-2))^2} \\[1em] = \sqrt{(-4)^2 + (-3)^2} \\[1em] = \sqrt{16 + 9} \\[1em] = \sqrt{25} \\[1em] = 5$

Thus, AC = BC

By formula,

Slope = $\dfrac{y$2 - y1}{x2 - x1}

Slope of AB = $\dfrac{-2 - 2}{6 - 3} = \dfrac{-4}{3}$

Slope of BC = $\dfrac{-5 - (-2)}{2 - 6} = \dfrac{-3}{-4} = \dfrac{3}{4}$

Slope of AB x Slope of BC = $\dfrac{-4}{3} \times \dfrac{3}{4}$ = -1

Hence, AB ⊥ BC

Therefore, A, B, C can be the vertices of a square.

(i) Slope of CD = Slope of AB = $-\dfrac{4}{3}$ (As they are parallel)

So, the equation of CD is

⇒ y – y₁ = m(x – x₁)

⇒ y - (-5) = $-\dfrac{4}{3}$(x – 2)

⇒ 3(y + 5) = -4(x - 2)

⇒ 3y + 15 = -4x + 8

⇒ 4x + 3y + 7 = 0 ………(1)

Slope of AD = Slope of BC = $\dfrac{3}{4}$ (As these lines are parallel)

So, the equation of the line AD is

⇒ y – y₁ = m(x – x₁)

⇒ y - 2 = $\dfrac{3}{4}$(x - 3)

⇒ 4(y – 2) = 3(x – 3)

⇒ 4y - 8 = 3x - 9

⇒ 3x - 4y = -8 + 9

⇒ 3x - 4y = 1 ……… (2)

Now, D is the point of intersection of CD and AD.

Solving (1) and (2),

Multiplying equation (1) by 4 and (2) by 3 and adding them we get,

⇒ 16x + 12y + 28 + 9x – 12y = 0 + 3

⇒ 25x = 3 - 28

⇒ 25x = -25

⇒ x = -1

Putting value of x in (1), we get

⇒ 4(-1) + 3y + 7 = 0

⇒ 3y - 4 + 7 = 0

⇒ 3y + 3 = 0

⇒ 3y = -3

⇒ y = -1

Hence, the co-ordinates of point D are (-1, -1).

(ii) From the equation (2)

The equation of the line AD is,

⇒ 3x – 4y = 1

⇒ 4y = 3x - 1.

Slope of AC = $\dfrac{-5 - 2}{2 - 3} = \dfrac{-7}{-1} = 7.$

Since, diagonals of a square are perpendicular to each other. So, product of their slopes = -1.

∴ Slope of AC × Slope of BD = -1

⇒ $7 \times$ Slope of BD = -1

⇒ Slope of BD = -$\dfrac{1}{7}$.

The equation of the diagonal BD is

⇒ y – y₁ = m(x – x₁)

⇒ y - (-2) = $-\dfrac{1}{7}$(x - 6)

⇒ 7(y + 2) = –1(x – 6)

⇒ 7y + 14 = -x + 6

⇒ x + 7y + 14 - 6 = 0

⇒ x + 7y + 8 = 0.

Hence, equation of line BD is x + 7y + 8 = 0 and AD = 4y = 3x - 1.