Mathematics
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Circles
Answer
Let PQ and RS be tangents to the circle at the ends of the diameter AB.
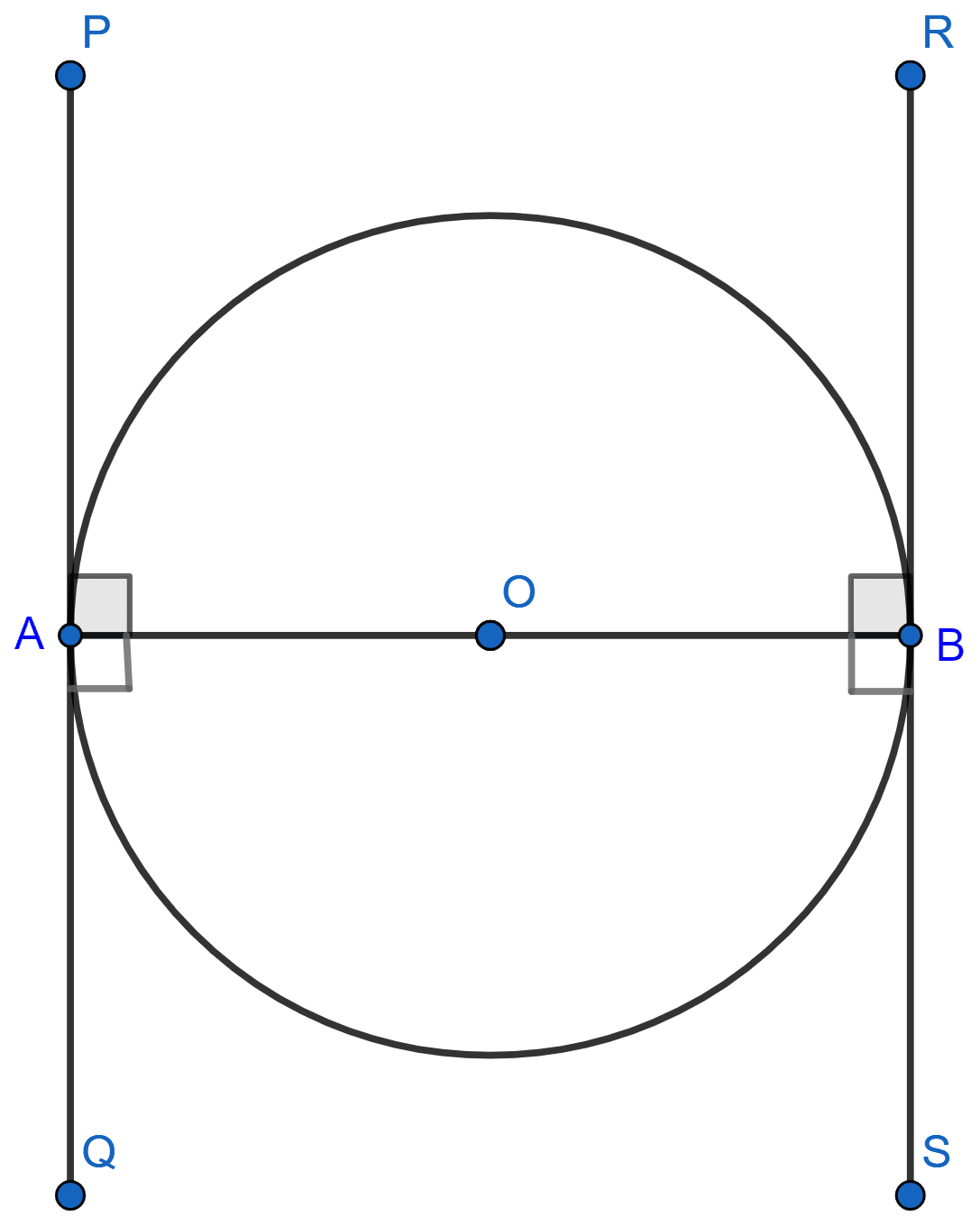
We know that,
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Thus, OA ⊥ PQ and OB ⊥ RS
∴ ∠PAO = 90°, ∠RBO = 90°, ∠OAQ = 90° and ∠OBS = 90°
Here, ∠OAQ is equal to ∠OBR and ∠PAO is equal to ∠OBS, which are two pairs of alternate interior angles.
If the alternate interior angles are equal, then lines PQ and RS should be parallel.
Hence, proved that tangents drawn at the ends of a diameter of a circle are parallel.
Answered By
Related Questions
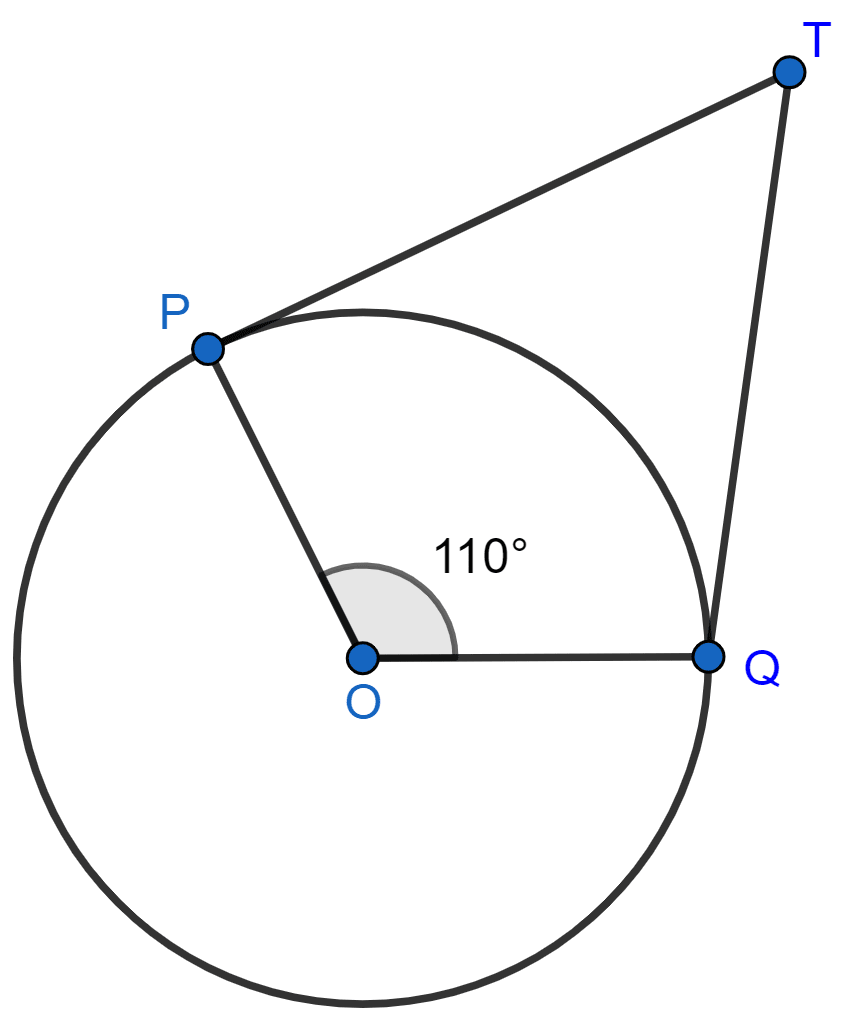
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
60°
70°
80°
90°
If tangents PA and PB from a point P to a circle with center O are inclined to each other at angle of 80°, then ∠POA is equal to
50°
60°
70°
80°
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.