Mathematics
Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
Similarity
Answer
Let two similar triangles be △ABC and △PQR.
We know that when triangles are similar ratio of corresponding sides are equal.
By property of ratio i.e.,
if then each ratio = .
So,
Since, AB + BC + AC = Perimeter of △ABC and PQ + QR + PR = Perimeter of △PQR. So,
Hence, proved.
Answered By
Related Questions
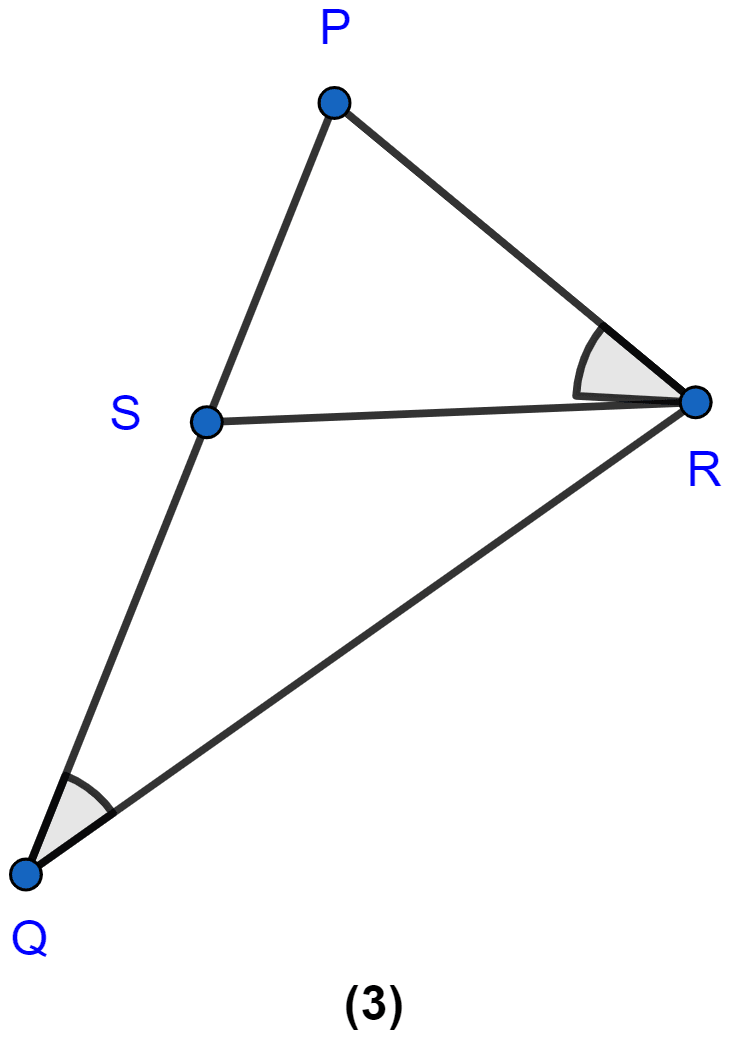
In the figure (3) given below, ∠ PQR = ∠ PRS. Prove that triangles PQR and PRS are similar. If PR = 8 cm, PS = 4 cm, calculate PQ.
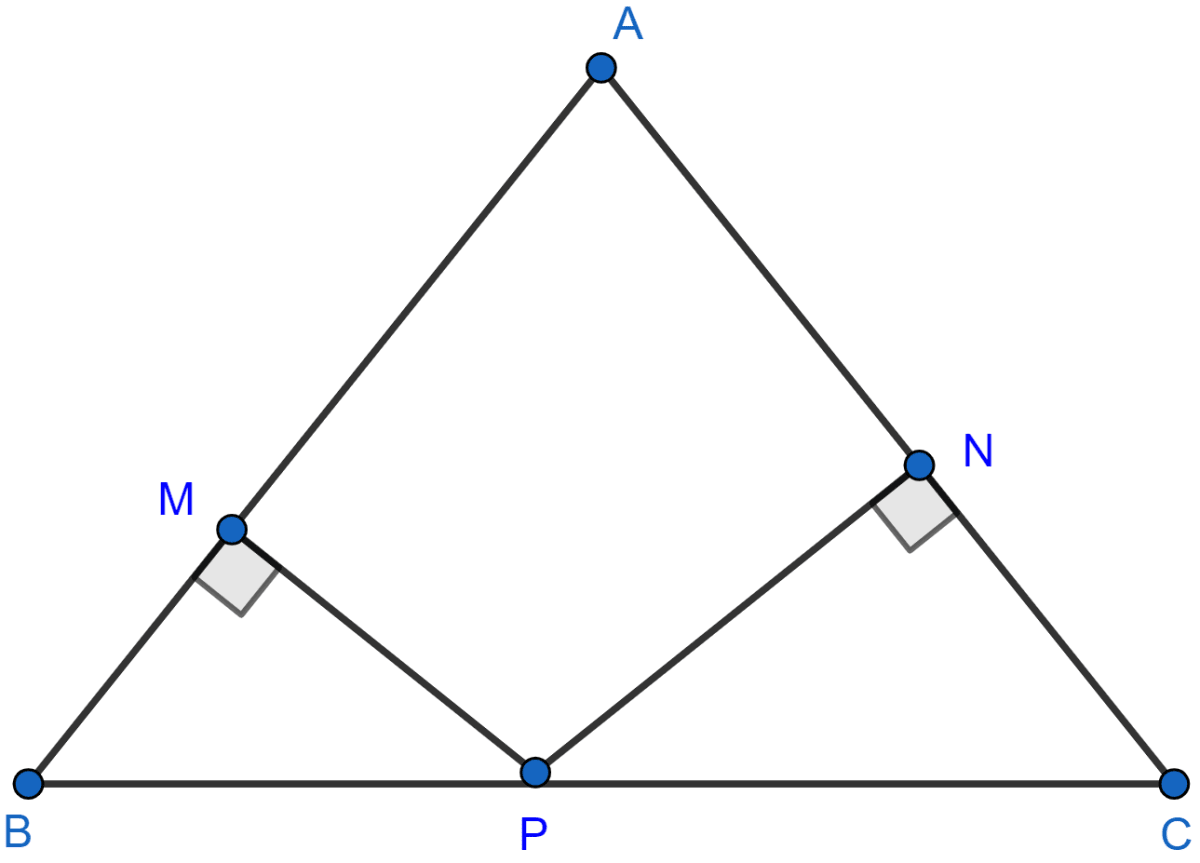
In the adjoining figure, ABC is a triangle in which AB = AC. P is a point on the side BC such that PM ⊥ AB and PN ⊥ AC. Prove that BM × NP = CN × MP.
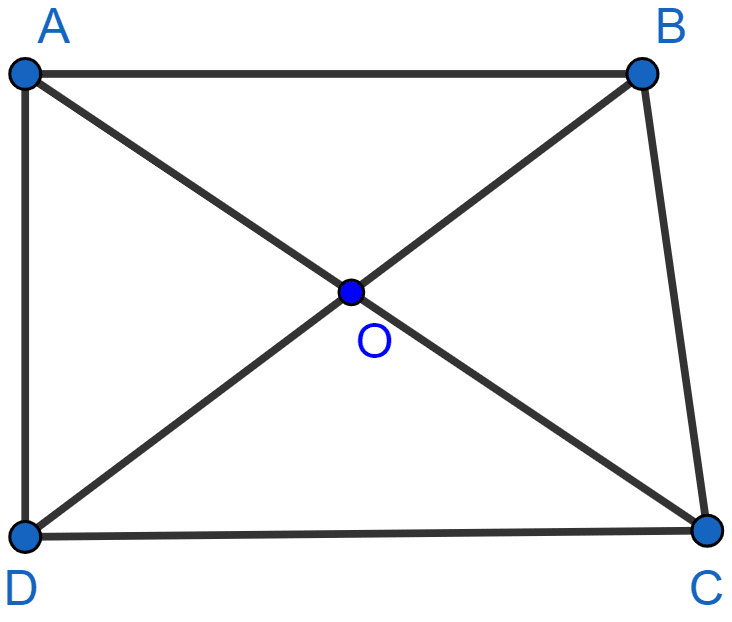
In the adjoining figure, ABCD is a trapezium in which AB ∥ DC. The diagonals AC and BD intersect at O. Prove that
Using the above result, find the value(s) of x if OA = 3x - 19, OB = x - 4, OC = x - 3 and OD = 4.
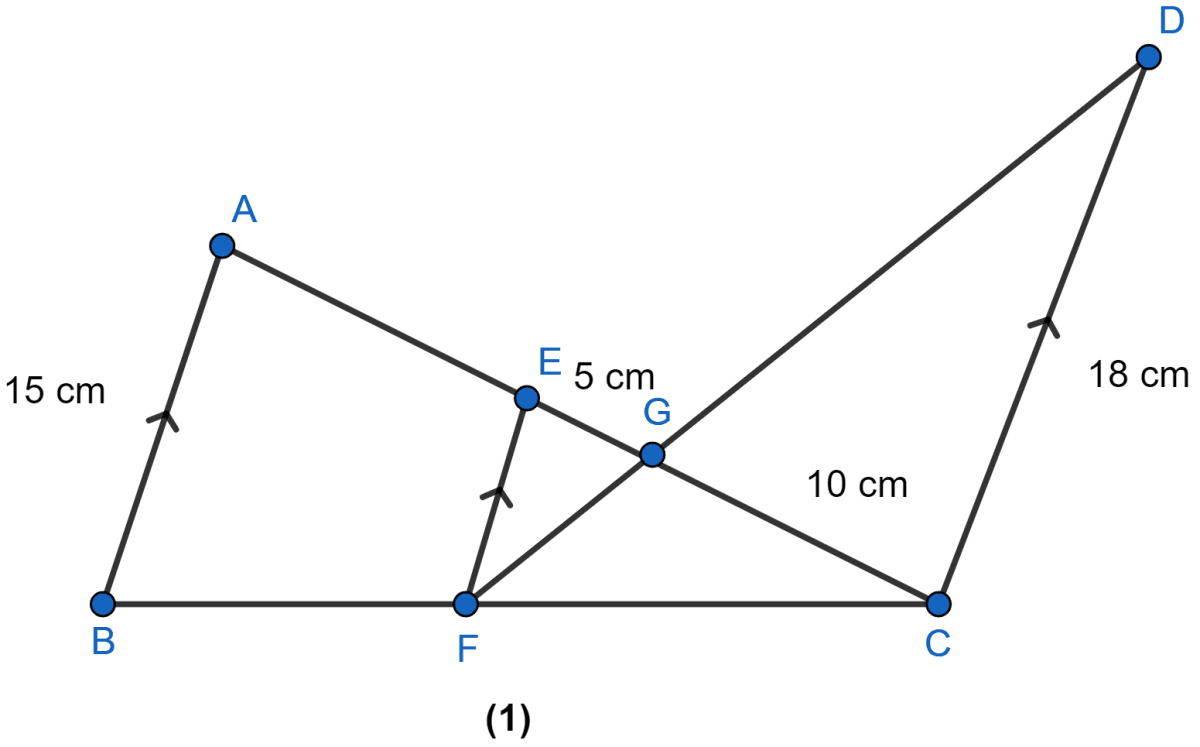
In the figure (1) given below, AB, EF and CD are parallel lines. Given that AB = 15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm. Calculate
(i) EF (ii) AC