Mathematics
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Answer
Let PQ be tangent to circle with center O.
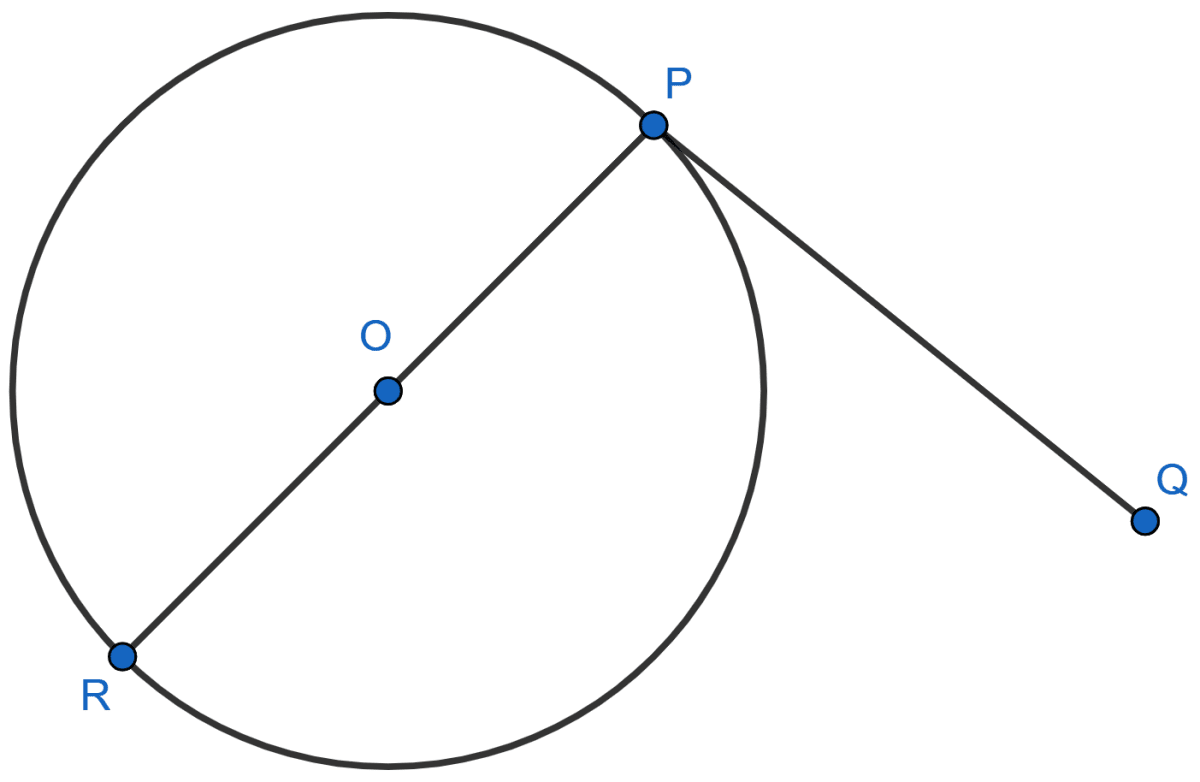
We know that,
Tangent at any point of a circle is perpendicular to the radius through the point of contact.
At the point of contact P, RP is perpendicular to the tangent PQ.
We know that,
Radius or diameter will always pass through the centre of the circle.
∴ PR passes through the centre O.
Hence it is proved that perpendicular PR of tangent PQ passes through centre O.
Related Questions
If tangents PA and PB from a point P to a circle with center O are inclined to each other at angle of 80°, then ∠POA is equal to
50°
60°
70°
80°
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.