Mathematics
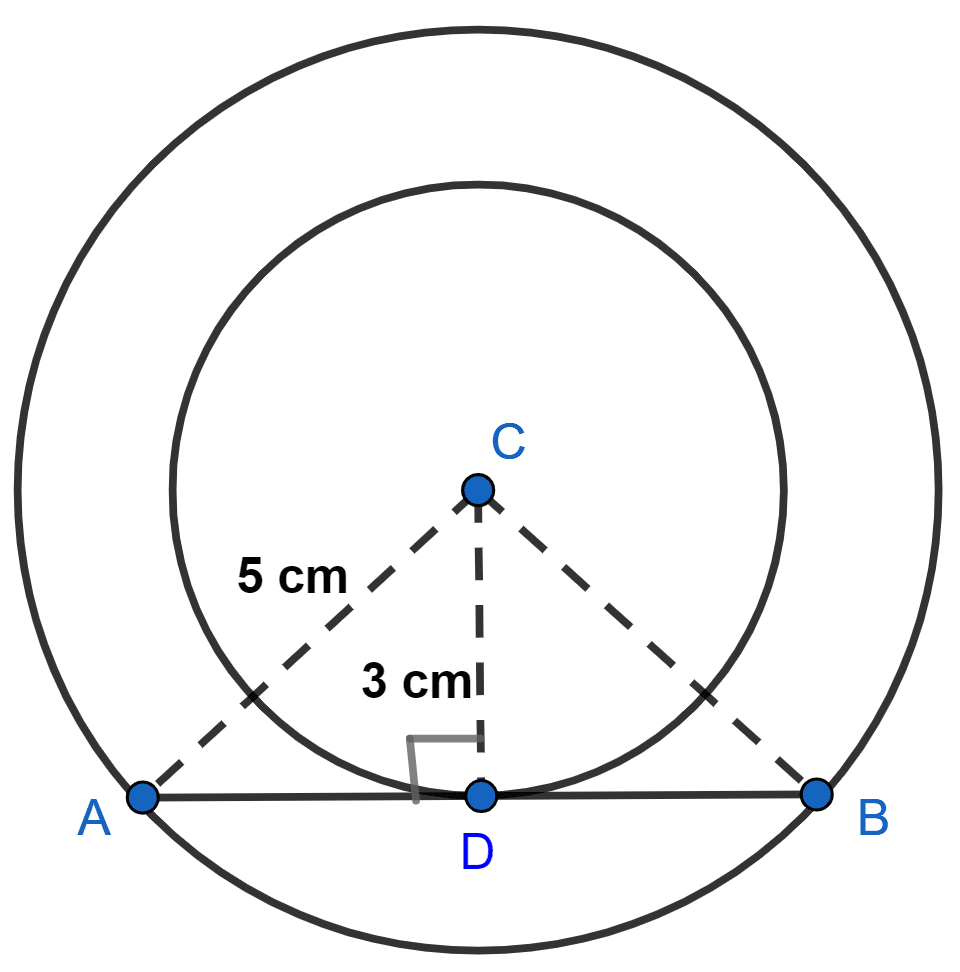
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Circles
3 Likes
Answer
Let C be the center of concentric circles and AB be the chord of larger circle touching smaller circle at point D.
So, AB can be the tangent to smaller circle.
We know that,
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ CD ⊥ AB.
In right angle triangle ACD,
By pythagoras theorem,
⇒ AC2 = AD2 + CD2
⇒ 52 = AD2 + 32
⇒ AD2 = 25 - 9
⇒ AD2 = 16
⇒ AD = = 4 cm.
In △DAC and △DBC,
⇒ ∠CDA = ∠CDB (Both equal to 90°)
⇒ AC = BC = 5 cm
⇒ CD = CD (Common)
∴ △DAC ≅ △DBC (By SAS axiom)
∴ AD = BD (By C.P.C.T.)
∴ BD = 4 cm.
AB = AD + BD = 4 + 4 = 8 cm.
Hence, length of required chord = 8 cm.
Answered By
2 Likes
Related Questions
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that :
AB + CD = AD + BC
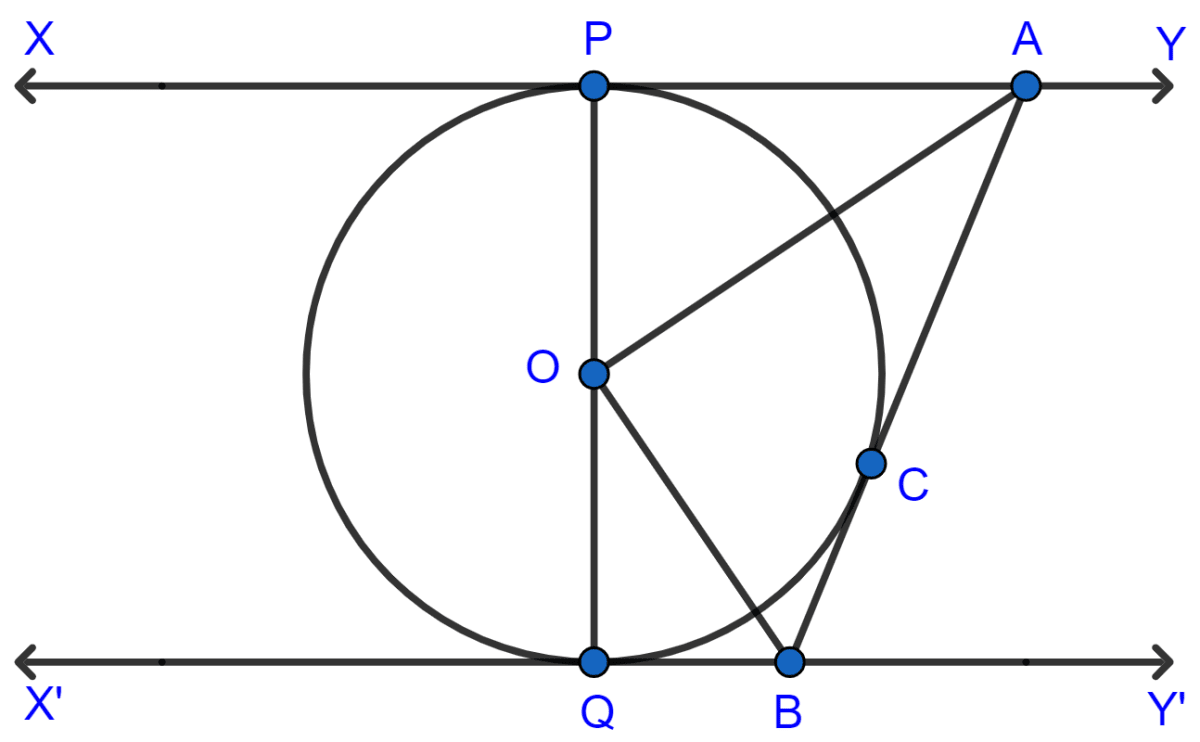
In the given figure, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' at B. Prove that ∠AOB = 90°.