Mathematics
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Circles
4 Likes
Answer
We know that,
The circles are congruent, their radii will be equal.
Let, there be two circles with center P and X with equal radius.
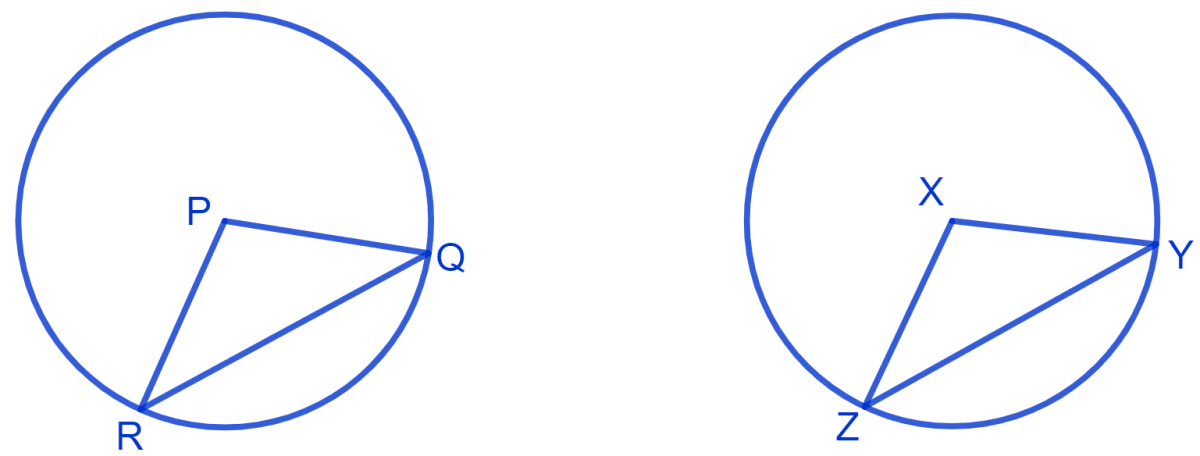
Since,
Chords of congruent circles subtend equal angles at their centres
∴ ∠QPR = ∠YXZ.
⇒ PR = PQ = XZ = XY
In ∆ PQR and ∆ XYZ,
⇒ PQ = XY (Radius of congruent circles are equal)
⇒ ∠QPR = ∠YXZ (Chords subtend equal angles at center)
⇒ PR = XZ (Radius of congruent circles are equal)
∴ ∆ PQR ≅ ∆ XYZ. (By S.A.S. congruence rule)
We know that,
Corresponding parts of congruent triangles are equal.
∴ QR = YZ (By C.P.C.T.)
Hence, proved that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answered By
2 Likes
Related Questions
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.