Prove that bisectors of any two adjacent angles of a parallelogram are at right angles.

Let AC be bisector of ∠A and BD be bisector of ∠B and they meet at point M.

From figure,

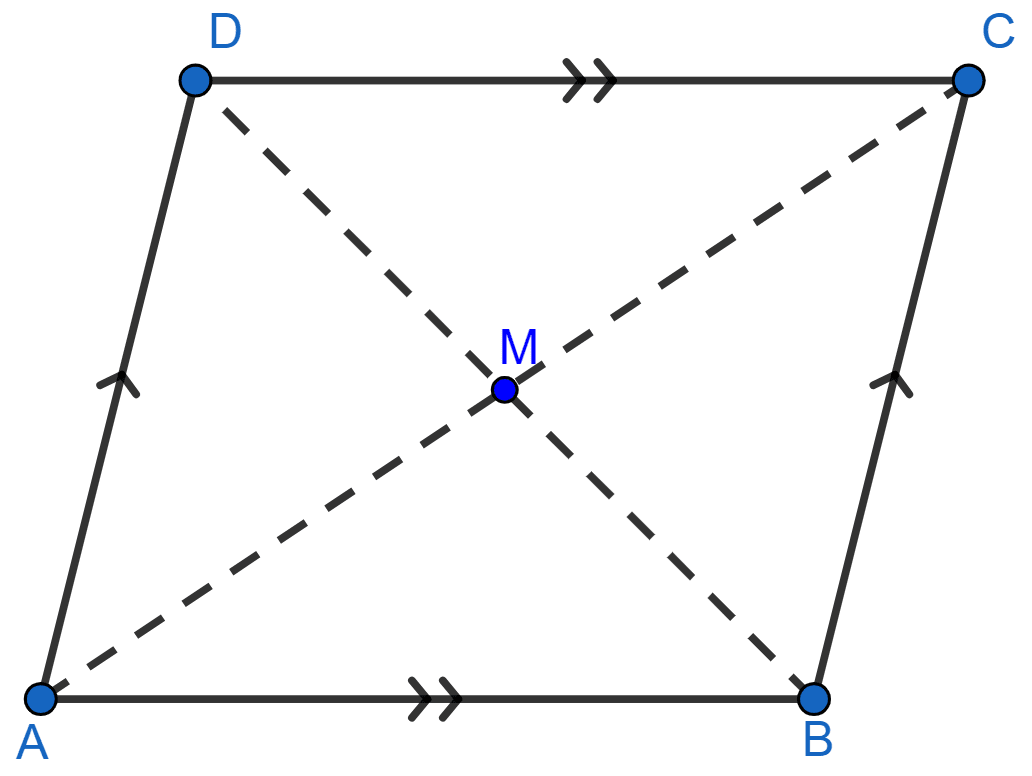
⇒ ∠A + ∠B = 180° (As AD || BC, sum of co-int ∠s = 180°)

⇒ $\dfrac{∠A + ∠B}{2} = \dfrac{180°}{2} = 90.$

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2} = 90°$

∴ ∠MAB + ∠MBA = 90° …….(i)

In △MAB,

⇒ ∠MAB + ∠MBA + ∠AMB = 180° (Sum of angles of triangle = 180°)

⇒ 90° + ∠AMB = 180° (from i)

⇒ ∠AMB = 180° - 90°

⇒ ∠AMB = 90°.

Hence, proved that bisectors of any two adjacent angles of a parallelogram are at right angles.