Mathematics
Prove that bisectors of any two opposite angles of a parallelogram are parallel.
Rectilinear Figures
55 Likes
Answer
Let the parallelogram be ABCD as shown in the figure below:
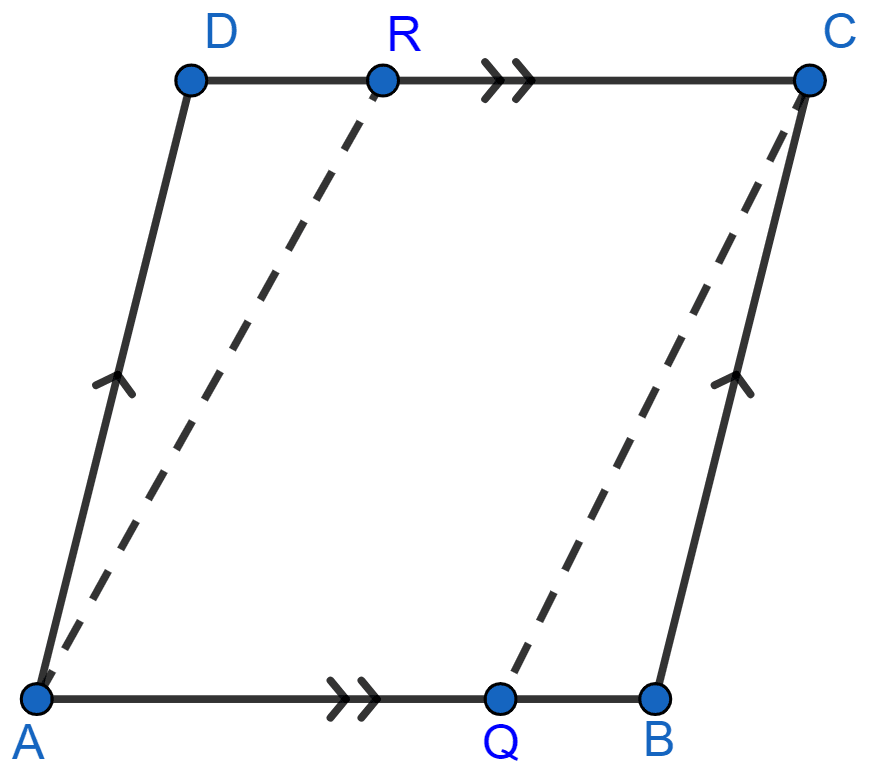
In parallelogram ABCD we have,
∠A = ∠C (Opposite angles are equal)
so,
∠DAR = ∠QCB (As AR bisects ∠A and QC bisects ∠C and ∠A = ∠C)
In △ADR and △CBQ,
⇒ ∠DAR = ∠QCB (Proved above)
⇒ AD = BC (Opposite sides of a || gm)
⇒ ∠D = ∠B (Opposite angles of a || gm)
Hence, △ADR ≅ △CBQ by ASA axiom.
∴ ∠DRA = ∠BQC (By C.P.C.T.) …….(i)
Also,
∠RAQ = ∠DRA (Alternate angles are equal) ………(ii)
From (i) and (ii) we get,
∠RAQ = ∠BQC (These are also corresponding angles)
Since, corresponding angles are equal, we can say that
AR || QC.
Hence, proved that bisectors of any two opposite angles of a parallelogram are parallel.
Answered By
16 Likes
Related Questions
ABCD is a parallelogram. If the diagonal AC bisects ∠A, then prove that :
(i) AC bisects ∠C
(ii) ABCD is a rhombus
(iii) AC ⊥ BD
Prove that bisectors of any two adjacent angles of a parallelogram are at right angles.
If the diagonals of a quadrilateral are equal and bisect each other at right angles, then prove that it is a square.
If ABCD is a rectangle in which the diagonal BD bisects ∠B, then show that ABCD is a square.