Mathematics
Prove that a cyclic parallelogram is a rectangle.
Circles
7 Likes
Answer
Let ABCD be the cyclic parallelogram.
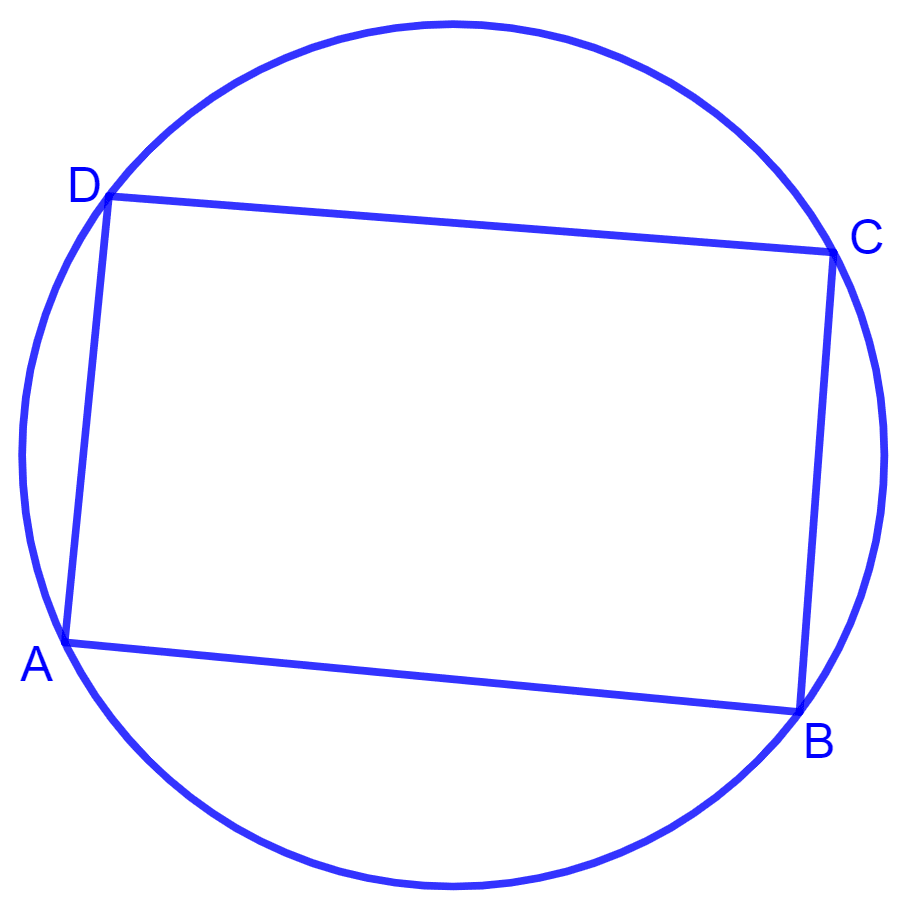
We know that opposite angles of a parallelogram are equal.
⇒ ∠A = ∠C …….(1)
⇒ ∠B = ∠D …….(2)
We know that the sum of opposite angles of a cyclic quadrilateral is 180°.
⇒ ∠A + ∠C = 180°
⇒ ∠A + ∠A = 180° (From equation (1))
⇒ 2∠A = 180°
⇒ ∠A =
⇒ ∠A = 90°.
We know that,
If one angle of a parallelogram is 90°, then it is a rectangle.
Thus, quadrilateral ABCD is a rectangle.
Hence, proved that a cyclic parallelogram is a rectangle.
Answered By
4 Likes
Related Questions
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
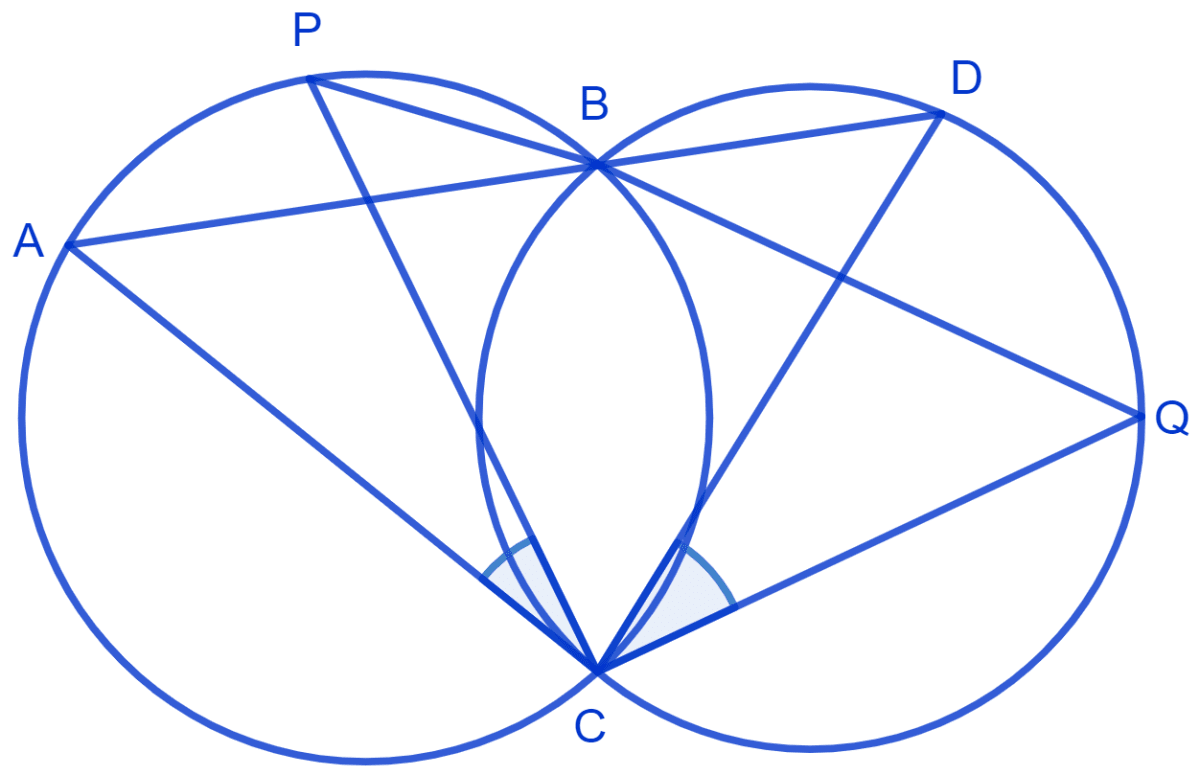
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ∠ACP = ∠QCD.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.