Mathematics
Perpendiculars are drawn from a point within an equilateral triangle to the three sides. Prove that the sum of the three perpendiculars is equal to the altitude of the triangle.
Theorems on Area
11 Likes
Answer
Since, ABC is an equilateral triangle. Let each side be x cm.
PN, PM, and PL are perpendicular on side AB, AC and BC respectively. AD is any altitude from point A on side BC.
Join PA, PB and PC.
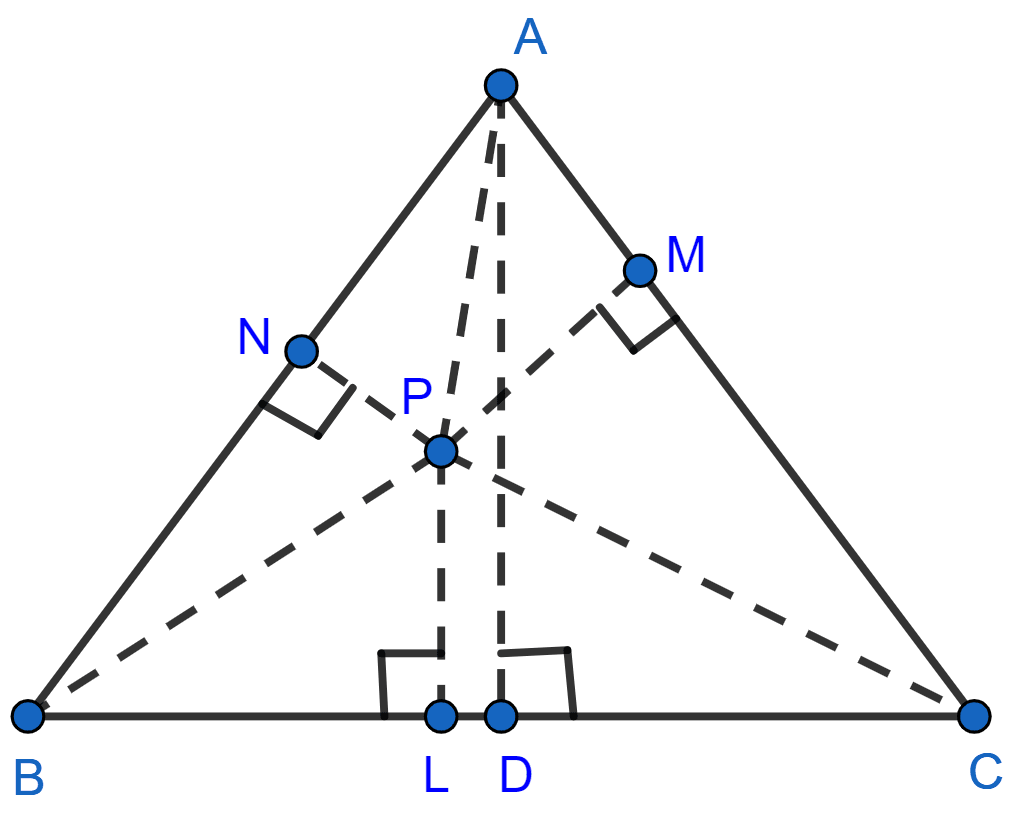
Area of ∆ABC = × Base × Altitude
= ……..(1)
Area of ∆APB = × AB × NP ……..(2)
Area of ∆APC = × AC × MP ……..(3)
Area of ∆BPC = × BC × LP ……..(4)
Adding (2), (3) and (4)
⇒ Area of (∆APB + ∆APC + ∆BPC) = × (AB × NP + AC × MP + BC × LP)
From figure,
∴ Area of ∆ABC = [NP + MP + LP] …….(5)
From (1) and (5),
× AD = × (NP + LP + MP)
⇒ AD = NP + LP + MP.
Hence, proved that the sum of three perpendiculars is equal to the altitude of the triangle.
Answered By
8 Likes
Related Questions
In the parallelogram ABCD, P is a point on the side AB and Q is a point on the side BC. Prove that
(i) area of ∆CPD = area of ∆AQD
(ii) area of ∆ADQ = area of ∆APD + area of ∆CPB.
If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.
In the adjoining figure, ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. If area of ∆DFB = 3 cm2, find the area of parallelogram ABCD.

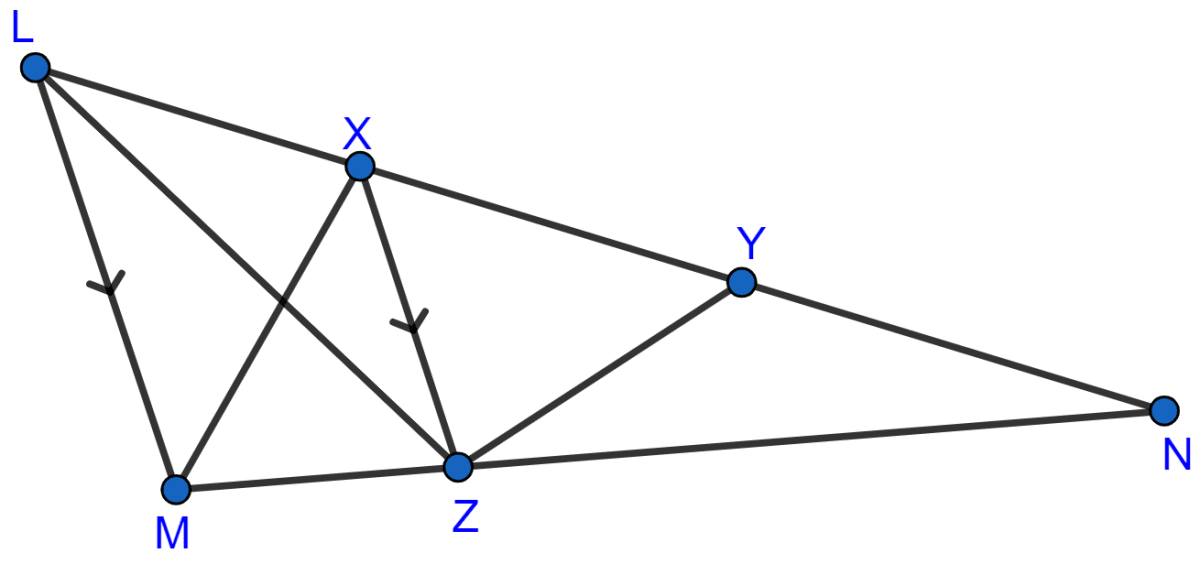
In the adjoining figure, X and Y are points on the side LN of triangle LMN. Through X, a line is drawn parallel to LM to meet MN at Z. Prove that area of ∆LZY = area of quad. MZYX.