Mathematics
P and Q are points on the sides AB and AC of triangle ABC. If AP = 3 cm, PB = 6 cm, AQ = 4.5 cm and QC = 9 cm, show that BC = 3 × PQ.
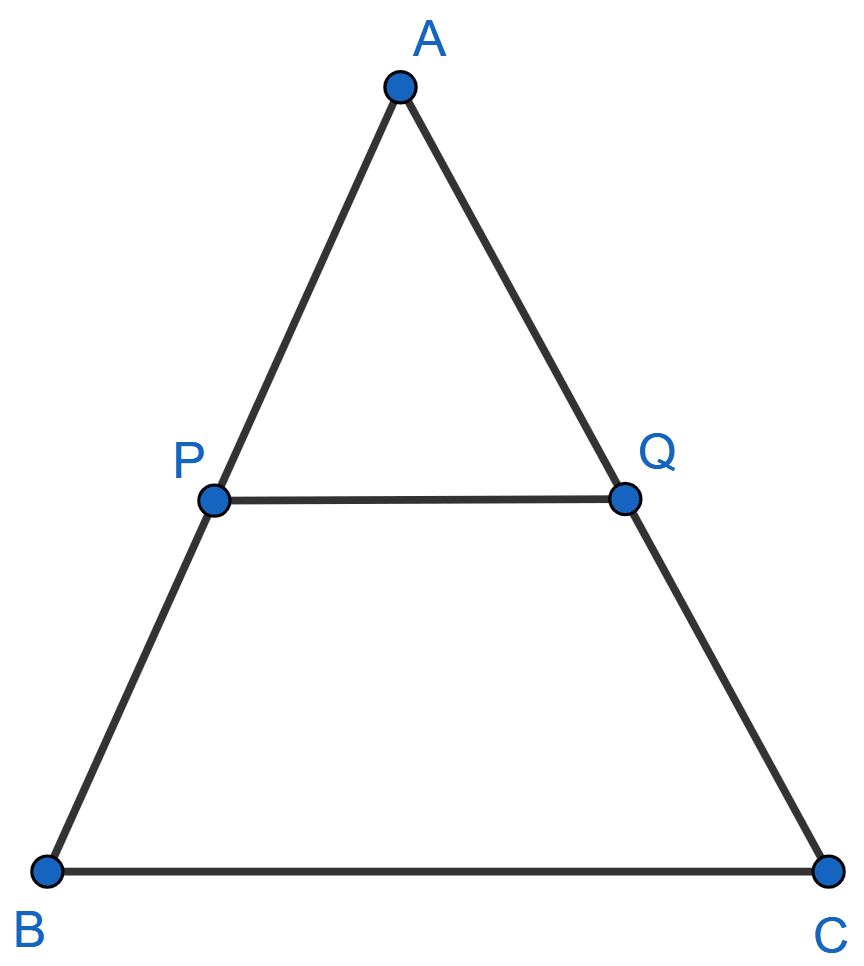
Similarity
2 Likes
Answer
Calculating,
.
So,
.
∴ PQ || BC (By converse of basic proportionality theorem)
In Δ APQ and Δ ABC
∠APQ = ∠ABC (corresponding angles are equal)
∠AQP = ∠ACB (corresponding angles are equal)
∴ Δ APQ ~ Δ ABC (By A.A. axiom)
From figure,
AB = AP + PB = 3 + 6 = 9 cm.
We know that,
In similar triangles ratio of corresponding sides are proportional.
Hence, proved that BC = 3 × PQ.
Answered By
2 Likes
Related Questions
The marks obtained (out of 100) by 400 students in an examination are given below :
Marks No. of students 0-10 10 10-20 20 20-30 22 30-40 40 40-50 54 50-60 76 60-70 80 70-80 58 80-90 28 90-100 12 Using a graph paper, draw an ogive for the above distribution. Use your graph to estimate :
(i) the median marks.
(ii) the number of students who obtained more than 80% marks in the examination.
(iii) the number of students who did not pass, if the pass percentage was 35.
The following table shows a record of the weights, in kilogram, of 100 pupil. Find the mean weight.
Weight Number of pupils 50-53 15 53-56 18 56-59 20 59-62 25 62-65 16 65-68 6 The speed of a boat in still water is 11 km per hour. It can go 12 km upstream and return downstream to the original point in 2 hours and 45 minutes. Find the speed of stream.
Solve :
13x - 5 < 15x + 4 < 7x + 12, x ∈ R. Represent the solution set on a real number line.